算法整理

April 19, 2025 169945

注意事项

`rust` 中 `dbg!` 超时

在 rust 中使用 dbg! 的时候，在题目判定时，可能会因为 dbg! 超时，提交代码的时候要去掉 dbg!

数组

双指针

第 27、977 题就是经典的双指针题目。

有序数组平方。

滑动窗口

注意，使用滑动窗口的时候，只用一个 for 循环代表滑动窗口的结尾，否则又会陷入两个 for 的困境。

长度最小的子数组

前缀和

1
2
3

for(int i = 1; i <= n; i++) {
    s[i] = s [i-1] + a[i];
}

Java 多组输入示例

import java.util.Scanner;

public class Main {
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt();
        int[] nums = new int[n + 1];
        int[] s = new int[n + 1];
        
        for (int i = 1; i <= n; i++) {
            nums[i] = scanner.nextInt();
            s[i] = s[i - 1] + nums[i];
        }
        
        while (scanner.hasNextInt()) {
            int a = scanner.nextInt();
            int b = scanner.nextInt();
            System.out.println(s[b+1] - s[a]);
        }
        scanner.close();
    }
}

模拟矩阵

走完一行或者一列对 x 和 y 进行处理，使得继续走下一行而不下标越界
走完一行或者一列对 x 和 y 进行处理，使得走到没有写数字的地方
走完一行或者一列对边界进行处理

class Solution {
    public int[][] generateMatrix(int n) {
        int [][]result = new int[n][n];
        int count = 1;
        int x = 0, y = 0;
        int xMax = n, yMax = n, xMin = 0, yMin = 0;
        while (count <= n * n) {
            // 向右
            while (y < yMax) {
                result[x][y] = count++;
                y++;
            }
            y--; // 能够向下走
            x++; // 走到没写过数字的地方
            xMin += 1; // 向右一行补充完向上少走一行

            // 向下
            while (x < xMax) {
                result[x][y] = count++;
                x++;
            }
            x--; // 能够向左走
            y--; // 走到没写过数字的地方
            yMax -= 1; // 向右少走一行

            // 向左
            while (y >= yMin) {
                result[x][y] = count++;
                y--;
            }
            y++; // 能够向右走
            x--; // 走到没写过数字的地方
            xMax -= 1; // 向下少走一行

            // 向上
            while (x >= xMin) {
                result[x][y] = count++;
                x--;
            }
            x++; // 能够向右走
            y++; // 走到没写过数字的地方
            yMin += 1; // 向左少走一行

        }
        return result;
    }
    
}

最大子数组和

dp[i] 代表以第 i 个元素结尾的最大子数组的和：

class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n + 1];
        int ans = nums[0];
        dp[0] = 0;
        for (int i = 1; i <= n; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i - 1], nums[i - 1]);
            ans = Math.max(ans, dp[i]);
        }
        return ans;
    }
}

合并区间

要点在于判断什么时候可以合并，什么时候不能合并：

先根据开头位置排序
下一个区间的开头大于当前末尾的时候不能合并
其他情况可以合并

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (a, b) -> { return a[0] - b[0]; });
        List<int[]> ans = new ArrayList<>();
        ans.add(intervals[0]);
        for (int i = 1; i < intervals.length; i++) {
            int right = ans.get(ans.size() - 1)[1];
            if (intervals[i][0] > right) { // 下一个的头部大于当前最后一个，不合并
                ans.add(intervals[i]);
            } else { // 可以合并
                right = Math.max(right, intervals[i][1]);
                ans.get(ans.size() - 1)[1] = right;
            }
        }
        return ans.toArray(new int[ans.size()][]);
    }
}

轮转数组

反转三次数组。

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        reverse(nums, 0, n - 1);
        reverse(nums, 0, (k % n) - 1);
        reverse(nums, k % n, n - 1);
    }

    private void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int tmp = nums[start];
            nums[start] = nums[end];
            nums[end] = tmp;
            start++;
            end--;
        }
    }
}

除自身以外数组的乘积

要求不使用除法，并且当前元素如果为 0 的时候，总和除以当前元素也用不了。

没有优化

要点在于将当前以外的乘积分为左边和右边部分，这样就可以划分并逐步计算得到答案。

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;
        int[] l = new int[n + 1], r = new int[n + 1];
        l[0] = 1;
        r[n] = 1;
        for (int i = 1; i <= n; i++) {
            l[i] = l[i - 1] * nums[i - 1];
        }

        for (int j = n - 1; j >= 1; j--) {
            r[j] = r[j + 1] * nums[j];
        }

        int[] ans = new int[n];

        for (int i = 0; i < n; i++) {
            ans[i] = l[i] * r[i + 1];
        }

        return ans;
    }
}

优化空间

用 ans 数组记录右边数组的乘积，然后用一个变量记录左边数组的乘积。

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;
        int[] ans = new int[n];
        ans[0] = 1;
        ans[n - 1] = nums[n - 1];

        for (int i = n - 2; i >= 0; i--) {
            ans[i] = ans[i + 1] * nums[i];
        }

        int l = 1;
        for (int i = 0; i < n; i++) {
            int r = 1;
            if (i < n - 1) r = ans[i + 1];
            ans[i] = l * r;
            l = l * nums[i];
        }

        return ans;
    }
}

缺失的第一个正数

要点在于

原地哈希，f(nums[i]) = nums[i] - 1
其他的在于防止死循环和保证所有数字都被 hash 过

class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            boolean isSwap = true;
            while (isSwap) {
                int hash = nums[i] - 1;
                if (0 <= hash && hash < n && i != hash && nums[hash] != nums[i]) { // 第3个和第4个条件防止死循环
                    swap(nums, i, hash);
                } else {
                    isSwap = false;
                }
            }

        }

        for (int i = 0; i < n; i++) {
            if (i + 1 != nums[i]) {
                return i + 1;
            }
        }

        return n + 1;
    }

    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

矩阵

矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

难点在于原地算法，否则很简单，模拟就好，模拟的时候注意不要跳过本来为 0 的元素。

旋转图像

要点在于：

做不到一步直接交换到位
先副对角线对称，然后上下对称

class Solution {
    public void rotate(int[][] matrix) {
        // 沿着副对角线对称，然后上下交换
        // 9 6 3
        // 8 5 2
        // 7 4 1

        // 找到每个元素的 swap 位置
        int n = matrix.length;
        // 沿着副对角线对称
        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= n - 1 - i; j++) {
                // 关于副对角线对称有 (i, j) <-> (n-1-i, n-1-j)
                swap(matrix, i, j, n - 1 - j, n - 1 - i);
            }
        }
        // 沿着 x 轴对称
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < n; j++) {
                // 关于 x 轴对称有 (i, j) <-> (n-1-i, j)
                swap(matrix, i, j, n - 1 - i, j);
            }
        }
    }

    public void swap(int[][] matrix, int i, int j, int x, int y) {
        int tmp = matrix[i][j];
        matrix[i][j] = matrix[x][y];
        matrix[x][y] = tmp;
    }
}

// 副对角线对称
// 0,0 -> n-1,n-1
// 0,1 -> n-2,n-1
// 0,n-1 -> 0,n-1
// 1,0 -> n-1,n-2

搜索二维矩阵 II

img

二分

每一行二分搜索

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        for (int[] nums : matrix) {
            if (Arrays.binarySearch(nums, target) >= 0) {
                return true;
            }
        }

        return false;
    }
}

总时间复杂度 O(m logn)

Z 字搜索

要点在于：

看矩阵右上角，左边严格小于，下面严格大于
所以每次可以排除掉一行或者一列，总时间复杂度 O(m + n)

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        // 看矩阵右上角，左边严格小于，下面严格大于
        int m = matrix.length;
        int n = matrix[0].length;
        int row = 0, col = n - 1;
        while (row < m && col >= 0) {
            if (target == matrix[row][col]) {
                return true;
            } else if (target > matrix[row][col]) {
                row++;
            } else { // target < matrix[row][col]
                col--;
            }
        }
        return false;
    }
}

双指针

移动零

10^4 O(n)

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

key：保证 right 在 left 左边。

盛最多水的容器

10^5 O(n)

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

思考：有两个变量决定盛水量：1. 左右的距离。 2. 较低的柱子高度。

左右的距离最左到最右最大，然后慢慢缩小。
如果移动较高的柱子，那么盛水量不会变大，但是如果移动较低的柱子，那么盛水量有可能会变大。

接雨水

2 * 10^4

img

1
2
3

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

key：某一处的雨水 = 全局左右最高柱子的最小值 - 当前处的高度

剩下的点就在求左右最高柱子处进行优化。

动态规划

将左右最高柱子的高度分别记为 leftMax，rightMax，并 O(n) 计算出这个数组的。

可以用动态规划求 left 和 right 的原因是这里的 left 和 right 表示的是全局最高，而柱状图中最大的矩形这道题中不是全局最低的。

需要注意的点是 初始值 和边界。

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int[] leftMax = new int[n];
        int[] rightMax = new int[n];
        leftMax[0] = height[0];
        for (int i = 1; i < n; i++) {
            leftMax[i] = Math.max(leftMax[i - 1], height[i]);
        }
        rightMax[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i--) {
            rightMax[i] = Math.max(rightMax[i + 1], height[i]);
        }
        int total = 0;
        for (int i = 1; i < n; i++) {
            total += Math.min(leftMax[i], rightMax[i]) - height[i];
        }
        return total;
    }
}

时间复杂度：O(n)，其中 n 是数组 height 的长度。计算数组 leftMax 和 rightMax 的元素值各需要遍历数组 height 一次，计算能接的雨水总量还需要遍历一次。

空间复杂度：O(n)，其中 n 是数组 height 的长度。需要创建两个长度为 n 的数组 leftMax 和 rightMax。

单调栈

双指针

动态规划计算 leftMax 和 rightMax 的时候需要遍历一次数组，能不能直接得到 leftMax 和 rightMax 而不遍历呢？这样就可以将得到 max 的复杂度降低为 O(1) 了。

与盛最多水的容器相同的思路，可以从两边的雨水向中间进行计算，这样可以 O(1) 得到

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int ans = 0;
        int left = 0, right = n - 1;
        int maxLeft = 0, maxRight = 0;
        while (left < right) {
            maxLeft = Math.max(maxLeft, height[left]);
            maxRight = Math.max(maxRight, height[right]);
            if (height[left] > height[right]) {
                ans += maxRight - height[right];
                right--;
            } else {
                ans += maxLeft - height[left];
                left++;
            }
        }
        return ans;
    }
}

滑动窗口

滑动窗口模板

// 外层循环扩展右边界，内层循环扩展左边界
for (int l = 0, r = 0 ; r < n ; r++) {
	// 当前考虑的元素
	while (l <= r && check()) { // 区间[left,right]不符合题意
        // 扩展左边界
    }
    // 区间[left,right]符合题意，统计相关信息
}

无重复字符的最长子串

5 * 10^4 级别

给定一个字符串 s ，请你找出其中不含有重复字符的最长子串的长度。

判断重复字符：Set
最长字串：滑动窗口

这道题官方解答为枚举所有起始位置，之后向右延申至不含重复字符的最长子串长度，如果包含重复字符，那么左指针持续移动到不含重复字符为止。

关键在于有重复字符的时候，是左指针持续地向右移动，而不是重新开始枚举，因为这个操作，使得时间复杂度为 O(n)，那么为什么这样不会漏掉答案呢？也就是说为什么这样一定会取到最优答案呢？

因为当右边要出现重复字母的的候，这个时候左指针到右指针的子串一定是对应了右指针不移动情况下的最优子串。

所以可以枚举右指针，并让左指针不断向右。

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Set<Character> set = new HashSet<>();
        int n = s.length(), l = 0, ans = 0;
        for (int r = 0; r < n; r++) {
            while (set.contains(s.charAt(r))) {
                set.remove(s.charAt(l));
                l++;
            }
            set.add(s.charAt(r));
            ans = Math.max(ans, r - l + 1);
        }
        return ans;
    }
}

找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的异位词的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

3 * 10^4 级别

与上一题相同，需要做以下操作：

判断异位词。
异位词子串。

确定异位词需要 O(n)，n 是字符串长度。

key：在这道题中，异位词和原词肯定是长度相同的，所以直接用固定长度的滑动窗口滑过去，这样时间复杂度为 O(n * m)。但是有更好的做法，就是当向右滑动的时候，删掉的是左面的字母，如果右边能够补齐，那么就说明是异位词，这样就可以 O(1) 判断异位词，再加上滑动的耗时，总计 O(m)。

Arrays.equals 可以判断两个数组相等。

统计好子数组的数目

给你一个整数数组 nums 和一个整数 k ，请你返回 nums 中好子数组的数目。

一个子数组 arr 如果有至少 k 对下标 (i, j) 满足 i < j 且 arr[i] == arr[j] ，那么称它是一个好子数组。

子数组 是原数组中一段连续非空的元素序列。

示例 1：

1
2
3

输入：nums = [1,1,1,1,1], k = 10
输出：1
解释：唯一的好子数组是这个数组本身。

示例 2：

输入：nums = [3,1,4,3,2,2,4], k = 2
输出：4
解释：总共有 4 个不同的好子数组：
- [3,1,4,3,2,2] 有 2 对。
- [3,1,4,3,2,2,4] 有 3 对。
- [1,4,3,2,2,4] 有 2 对。
- [4,3,2,2,4] 有 2 对。

提示：

1 <= nums.length <= 10^5
1 <= nums[i], k <= 10^9

核心思路：

如果窗口中有 c 个元素 x，再进来一个 x，会新增 c 个相等数对。
如果窗口中有 c 个元素 x，再去掉一个 x，会减少 c−1 个相等数对。
用一个哈希表 cnt 维护子数组（窗口）中的每个元素的出现次数，以及相同数对的个数 pairs。

外层循环：从小到大枚举子数组右端点 right。现在准备把 x=nums[right] 移入窗口，那么窗口中有 cnt[x] 个数和 x 相同，所以 pairs 会增加 cnt[x]。然后把 cnt[x] 加一。

内层循环：如果发现 pairs≥k，说明子数组符合要求，右移左端点 left，先把 cnt[nums[left]] 减少一，然后把 pairs 减少 cnt[nums[left]]。

内层循环结束后，[left,right] 这个子数组是不满足题目要求的，但在退出循环之前的最后一轮循环，[left−1,right] 是满足题目要求的。由于子数组越长，越能满足题目要求，所以除了 [left−1,right]，还有 [left−2,right],[left−3,right],…,[0,right] 都是满足要求的。也就是说，当右端点固定在 right 时，左端点在 0,1,2,…,left−1 的所有子数组都是满足要求的，这一共有 left 个。

class Solution {
    public long countGood(int[] nums, int k) {
        long ans = 0;
        Map<Integer, Integer> cnt = new HashMap<>();
        int pairs = 0;
        int left = 0;
        for (int x : nums) {
            int c = cnt.getOrDefault(x, 0);
            pairs += c; // 进
            cnt.put(x, c + 1);
            while (pairs >= k) {
                x = nums[left];
                c = cnt.get(x);
                pairs -= c - 1; // 出
                cnt.put(x, c - 1);
                left++;
            }
            ans += left;
        }
        return ans;
    }
}

区间

合并区间

先排序，排序之后放入第一个元素，然后判断后续的开头是不是小于第一个元素的结尾，如果是的话就连起来，否则就形成新的区间。

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (a1, a2) -> {
            return a1[0] - a2[0];
        });
        List<int[]> ans = new ArrayList<>();
        ans.add(intervals[0]);
        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] > ans.get(ans.size() - 1)[1]) {
                ans.add(intervals[i]);
            } else {
                int right = ans.get(ans.size() - 1)[1];
                right = Math.max(right, intervals[i][1]);
                ans.get(ans.size() - 1)[1] = right;
            }
        }
        return ans.toArray(new int[ans.size()][]);
    }
}

区间列表的交集

因为两个列表里都为不相交且已经排序好的区间，我们可以使用双指针逐个检查重合区域

对于两个区间arr1=[left1,right1]，arr2=[left2,right2]
判断重合：

若两个区间arr1与arr2相交，那么重合区域为[max(left1,left2),min(right1,right2)]
若不相交，则right1<left2或right2<left1，那么求得的重合区域max(left1,left2)的值会比min(right1,right2)大，可以通过比较两个值来判断是否重合
移动指针：

假设right1<right2，因为区间列表为不相交且已经排序好的，则arr1不可能与secondList中arr2以后的任何区间相交。所以每次优先移动当前区间尾段较小的指针 (right2<right1同理)
若right1==right2，因为列表各个区间不相交，arr1与arr2都不可能与之后的区间有交集，可以移动任意一个

class Solution {
    public int[][] intervalIntersection(int[][] firstList, int[][] secondList) {
        List<int[]> ans = new ArrayList();
        int i = 0, j = 0;
        int n1 = firstList.length, n2 = secondList.length;

        while (i < n1 && j < n2) {
            int[] arr1 = firstList[i];
            int[] arr2 = secondList[j];

            int l = Math.max(arr1[0], arr2[0]);
            int r = Math.min(arr1[1], arr2[1]);

            if (l <= r) ans.add(new int[]{l, r});

            if (arr1[1] < arr2[1]) i++;
            else j++;

        }

        return ans.toArray(new int[ans.size()][]);
    }
}

链表

链表对于有插入、交换或者删除的操作的时候，一般加一个虚拟头节点更好处理。

203.移除链表元素

707.设计链表

206.翻转链表

19.删除链表的倒数第 N 个结点

K 个一组翻转链表

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

Key：关键在于写一个 reverse 函数逆转从 head 到 tail 的链表。其中 reverse 函数可以返回逆转后的最后一个节点。还有需要维护返回的节点。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (k == 1) return head;
        boolean first = true;
        ListNode dummy = new ListNode(0, head), cur = head, pre = dummy, ret = null;
        int count = 0;
        while (cur != null) {
            count++;
            if (count == k) {
                if (first) {
                    ret = cur;
                    first = false;
                }
                pre = reverse(pre, head, cur);
                head = pre.next;
                cur = pre;
                count = 0;
            }
            cur = cur.next;
        }
        return ret;
    }

    // 逆转从 head 到 tail 的链表，pre 是 head 的前一个结点
    // 返回逆转后的最后一个节点，其实就是 head，这一组的最后一个节点是下一组的 pre
    private ListNode reverse(ListNode pre, ListNode head, ListNode tail) {
        // pre -> head -> cur -> tail
        ListNode cur = head.next, retTail = head;
        head.next = tail.next;
        while (cur != tail) { // tail 之前的节点全部头插法插到到 pre 之后
            ListNode next = cur.next;
            pre.next = cur;
            cur.next = head;
            head = cur;
            cur = next;
        }
        // 把 tail 也插到头部
        pre.next = tail;
        tail.next = head;
        return retTail;
    }
}

排序链表

要点在于排序 + 链表操作

题目的进阶问题要求达到 O(nlogn) 的时间复杂度和 O(1) 的空间复杂度，时间复杂度是 O(nlogn) 的排序算法包括归并排序、堆排序和快速排序（快速排序的最差时间复杂度是 O(n^2)），其中最适合链表的排序算法是归并排序。

归并排序基于分治算法。最容易想到的实现方式是自顶向下的递归实现，考虑到递归调用的栈空间，自顶向下归并排序的空间复杂度是 O(logn)。如果要达到 O(1) 的空间复杂度，则需要使用自底向上的实现方式。=

递归写法：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode sortList(ListNode head) {
        if (head == null || head.next == null) return head;
        ListNode mid = findMiddle(head);
        ListNode rightHead = mid.next;
        mid.next = null; // 断开链表

        // 排序
        ListNode left = sortList(head);
        ListNode right = sortList(rightHead);
        
        // 合并有序链表
        return mergeList(left, right);
    }

    private ListNode mergeList(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;
        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                cur.next = l1;
                l1 = l1.next;
            } else {
                cur.next = l2;
                l2 = l2.next;
            }
            cur = cur.next;
        }
        // 接上剩余链表，这里不需要用 while，因为肯定要么 l1 要么 l2 剩余，剩余部分本来就是接好的
        if (l1 != null) {
            cur.next = l1;
        }

        if (l2 != null) {
            cur.next = l2;
        }

        return dummy.next;
    }

    private ListNode findMiddle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head.next; // 重要！fast 从 head.next 开始，确保 slow 指向中点或者左中点
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }
}

迭代写法：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    // 1. 获取链表长度
    // 2. 设置合并的长度（step）
    // 3. 合并根据长度划分的所有链表
    // 4. step *= 2
    public ListNode sortList(ListNode head) {
        ListNode dummy = new ListNode(0, head);
        int length = listLength(head);
        for (int step = 1; step < length; step *= 2) {
            ListNode cur = dummy.next;
            ListNode newTail = dummy;
            while (cur != null) {
                // 从 cur 开始，分割出两段长为 step 的链表，头节点分别为 head1 和 head2
                ListNode head1 = cur;
                ListNode head2 = splitList(head1, step);
                // 下一轮的起点，也是为了分割开链表
                cur = splitList(head2, step); 
                // 合并两段长度为 step 的链表
                ListNode merged = mergeList(head1, head2);
                // 找到下一个要合并的链表的 head
                int len = 0;
                ListNode curr = merged;
                while(len < step * 2 && curr.next != null) {
                    len++;
                    curr = curr.next;
                }
                // 合并后的头节点插入到 newTail 后面
                newTail.next = merged;
                newTail = curr;
            }
        }
        return dummy.next;
    }

    private ListNode splitList(ListNode head, int size) {
        ListNode cur = head;
        // nextHead 的前一个节点，用于断开链表
        for (int i = 0; i < size - 1 && cur != null; i++) {
            cur = cur.next;
        }

        if (cur == null || cur.next == null) return null;

        ListNode nextHead = cur.next;
        cur.next = null; // 断开链表
        return nextHead;
    }

    private int listLength(ListNode head) {
        int length = 0;
        while (head != null) {
            head = head.next;
            length++;
        }
        return length;
    }

    // 返回合并链表的头节点
    private ListNode mergeList(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;
        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                cur.next = l1;
                l1 = l1.next;
            } else {
                cur.next = l2;
                l2 = l2.next;
            }
            cur = cur.next;
        }
        // 接上剩余链表，这里要用 while，因为肯定要么 l1 要么 l2 剩余，剩余部分本来就是接好的
        if (l1 != null) {
            cur.next = l1;
        }

        if (l2 != null) {
            cur.next = l2;
        }

        return dummy.next;
    }
}

合并 K 个升序链表

朴素做法

用一个数组存储所有的 head，然后每次取出所有数组的最小值，然后插入到链表最后面。

每次取出最小值，复杂度为 O(k)，然后一共要取 k n 次，n 是最长链表的长度，这样时间复杂度为 O(k^2 n)，每次取出最小值的时候，有比较被浪费掉了。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;
        ListNode[] head = new ListNode[lists.length];
        int allLength = 500 * 10000;
        for (int i = 0; i < lists.length; i++) {
            head[i] = lists[i];
        }

        int i = 0;
        while (i < allLength) {
            int minVal = 0x3f3f3f3f;
            int minIndex = -1;
            for (int j = 0; j < lists.length; j++) {
                if (head[j] != null && minVal > head[j].val) {
                    minVal = head[j].val;
                    minIndex = j;
                }
            }
            // 所有链表都为空
            if (minIndex == -1) break;
            cur.next = head[minIndex];
            cur = cur.next;
            head[minIndex] = head[minIndex].next;
            i++;
        }
        return dummy.next;
    }
}

二分做法

img

复杂度计算：

image-20250202004335203

链表两两合并避免比较浪费，左闭右闭实现：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        return mergeLists(lists, 0, lists.length - 1);
    }

    private ListNode mergeLists(ListNode[] lists, int l, int r) {
        if (l == r) return lists[l];
        if (l > r) return null;
        int mid = l + (r - l) / 2;
        // 左闭右闭
        return mergeTwoLists(mergeLists(lists, l, mid), mergeLists(lists, mid + 1, r));
    }

    private ListNode mergeTwoLists(ListNode a, ListNode b) {
        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;
        while (a != null && b != null) {
            if (a.val <= b.val) {
                cur.next = a;
                a = a.next;
            } else {
                cur.next = b;
                b = b.next;
            }
            cur = cur.next;
        }

        if (a != null) cur.next = a;
        if (b != null) cur.next = b;

        return dummy.next;
    }
}

左闭右开实现：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        return mergeLists(lists, 0, lists.length);
    }

    private ListNode mergeLists(ListNode[] lists, int l, int r) {
        if (l >= r) return null;
        if (r - l == 1) return lists[l];
        int mid = l + (r - l) / 2;
        // 左闭右开
        return mergeTwoLists(mergeLists(lists, l, mid), mergeLists(lists, mid, r));
    }

    private ListNode mergeTwoLists(ListNode a, ListNode b) {
        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;
        while (a != null && b != null) {
            if (a.val <= b.val) {
                cur.next = a;
                a = a.next;
            } else {
                cur.next = b;
                b = b.next;
            }
            cur = cur.next;
        }

        if (a != null) cur.next = a;
        if (b != null) cur.next = b;

        return dummy.next;
    }
}

二叉树

二叉树的中序遍历

递归做法：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> list = new ArrayList<>();

    public List<Integer> inorderTraversal(TreeNode root) {
        helper(root);
        return list;
    }

    private void helper(TreeNode root) {
        if (root == null) {
            return;
        }
        helper(root.left);
        list.add(root.val);
        helper(root.right);
    }
}

非递归做法，用一个栈模拟递归栈。

前序遍历是中左右，如果还有左子树就一直向下找。完了之后再返回从最底层逐步向上向右找。

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                list.add(root.val);
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            root = root.right;
        }
        return list;
    }
}

中序是左中右，如果还有左子树就一直向下找，直到左边最底部，然后处理节点：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            list.add(root.val);
            root = root.right;
        }
        return list;
    }
}

前序是先中间，再左边然后右边，而这里是先中间，再后边然后左边。那我们完全可以改造一下前序遍历，得到序列new_seq之后再reverse一下就是想要的结果了：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                list.add(root.val);
                stack.push(root);
                root = root.right;
            }
            root = stack.pop();
            root = root.left;
        }
        Collections.reverse(list);
        return list;
    }
}

二叉树的最大深度

要点在于如何记录深度，递归的时候可以通过传参解决：

class Solution {
    int maxDepth = 0;

    public int maxDepth(TreeNode root) {
        helper(root, 0);
        return maxDepth;
    }

    private void helper(TreeNode root, int depth) {
        if (root == null) {
            maxDepth = Math.max(maxDepth, depth);
            return;
        }
        helper(root.left, depth + 1);
        helper(root.right, depth + 1);
    }
}

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}

反转二叉树

class Solution {
    public TreeNode invertTree(TreeNode root) {
        helper(root);
        return root;
    }

    private TreeNode helper(TreeNode root) {
        if (root == null) return null;
        TreeNode left = helper(root.right);
        TreeNode right = helper(root.left);
        root.left = left;
        root.right = right;
        return root;
    }
}

对称二叉树

这里注意条件是 left.val == right.val && helper(left.left, right.right) && helper(left.right, right.left) ，因为对称是中心轴对称，而不是左右相等。

class Solution {
    List<Integer> list = new ArrayList<>();
    public boolean isSymmetric(TreeNode root) {
        return helper(root.left, root.right);
    }

    private boolean helper(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true;
        }
        if (left == null || right == null) {
            return false;
        }
        return left.val == right.val
            && helper(left.left, right.right)
            && helper(left.right, right.left);
    }
}

二叉树的直径

二叉树的直径 = 最深左子树深度 + 最深右子树深度

class Solution {
    int ans = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        helper(root);
        return ans;
    }

    private int helper(TreeNode root) {
        if (root == null) return 0;
        int leftMax = helper(root.left);
        int rightMax = helper(root.right);
        ans = Math.max(ans, leftMax + rightMax);
        return Math.max(leftMax, rightMax) + 1;
    }
}

二叉树层序遍历

我的做法：先序遍历（root，左，右）的时候记住 depth 存到 map 中，然后最后把 map 中的数组组合起来：

class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Map<Integer, List<Integer>> map = new HashMap<>();

    public List<List<Integer>> levelOrder(TreeNode root) {
        int depth = helper(root, 0);
        for (int i = 0; i < depth; i++) {
            ans.add(map.get(i));
        }
        return ans;
    }

    private int helper(TreeNode root, int depth) {
        if (root == null) return depth;
        List<Integer> arr = map.getOrDefault(depth, new ArrayList<Integer>());
        arr.add(root.val);
        map.put(depth, arr);
        int leftMax = helper(root.left, depth + 1);
        int rightMax = helper(root.right, depth + 1);
        return Math.max(leftMax, rightMax);
    }
}

bfs 做法：

root 入队列
队列不为空的时候
- 求当前队列长度 $s_i$
- 取 $s_i$ 个元素进行拓展，进入下一次迭代

它和普通广度优先搜索的区别在于，普通广度优先搜索每次只取一个元素拓展，而这里每次取 $s_i$ 个元素。在上述过程中的第 $i$ 次迭代得到了二叉树第 $i$ 层的 $s_i$ 个元素。（说白了就是每次迭代的时候把下一层级的所有元素都加到队列里面，这样每一次迭代整个队列元素的时候就是一个层级的所有元素）

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ans = new ArrayList<>();
        if (root == null) return ans;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> list = new ArrayList<>();
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode front = queue.poll();
                if (front.left != null) queue.offer(front.left);
                if (front.right != null) queue.offer(front.right);
                list.add(front.val);
            }
            ans.add(list);
        }
        return ans;
    }
}

将有序数组转换为二叉搜索树

递归建树：

1 <= nums.length <= 10^4
-10^4 <= nums[i] <= 10^4
nums 按 严格递增 顺序排列

image-20250205185730436

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return helper(nums, 0, nums.length);
    }

    private TreeNode helper(int[] nums, int left, int right) {
        if (left >= right) return null;
        int mid = left + (right - left) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = helper(nums, left, mid);
        root.right = helper(nums, mid + 1, right);
        return root;
    }
}

验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

这里有一个问题是需要判断所有的子节点都大于或者都小于根节点。

二叉搜索树的中序遍历是递增的。所以可以中序遍历，之后每个元素都小于前一个元素，则是二叉搜索树。

递归写法：

class Solution {
    List<Integer> list = new ArrayList<>();

    public boolean isValidBST(TreeNode root) {
        helper(root);
        for (int i = 0; i < list.size() - 1; i++) {
            if (list.get(i) >= list.get(i + 1)) {
                return false;
            }
        }
        return true;
    }

    private void helper(TreeNode root) {
        if (root == null) return;
        helper(root.left);
        list.add(root.val);
        helper(root.right);
    }
}

递归写法2：

class Solution {
    long left = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        return helper(root);
    }

    private boolean helper(TreeNode root) {
        if (root == null) return true;
        boolean l = helper(root.left);
        boolean tmp = left < root.val;
        left = root.val;
        boolean r = helper(root.right);
        return l && r && tmp;
    }
}

递归写法3：

class Solution {
    public boolean isValidBST(TreeNode root) {
        return helper(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    private boolean helper(TreeNode root, long lower, long upper) {
        if (root == null) return true;
        if (root.val <= lower || root.val >= upper) return false;
        return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);
    }
}

迭代写法：

class Solution {
    public boolean isValidBST(TreeNode root) {
        return helper(root);
    }

    private boolean helper(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        long left = Long.MIN_VALUE;
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if (left >= root.val) return false;
            left = root.val;
            root = root.right;
        }
        return true;
        
    }
}

二叉搜索树中第 K 小的元素

和验证二叉搜索树一样，在最外层存储一下状态。

class Solution {
    int count = 0, target; // 存储状态
    public int kthSmallest(TreeNode root, int k) {
        target = k;
        return helper(root);
    }

    private int helper(TreeNode root) {
        if (root == null) return -1; 
        int left = helper(root.left);
        if (left != -1) return left;
        count++;
        if (target == count) {
            return root.val;
        }
        int right = helper(root.right);
        if (right != -1) return right;
        return -1;
    }
}

二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

层序遍历中最右面的那个元素就是答案，放进去就好了。

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        if (root == null) return ans;
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
                if (i == size - 1) {
                    ans.add(node.val);
                }
            }
        }
        return ans;
    }
}

二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

递归

先序遍历二叉树，然后记录 last，然后修改 last 的 left 和 right，但是这样会栈溢出。

原因是递归遍历 root.left 的时候，root.right 被改成了 root.left 导致死循环，保存一下状态就好了。

class Solution {
    private TreeNode last;
    public void flatten(TreeNode root) {
        last = new TreeNode(0, null, root);
        helper(root);
    }

    private void helper(TreeNode root) {
        if (root == null) return;
        TreeNode left = root.left;
        TreeNode right = root.right;
        last.left = null;
        last.right = root;
        last = root;
        helper(left);
        helper(right);
    }
}

迭代1

迭代写法，这里注意是第三种先序遍历的方法（递归，迭代1，迭代2），注意先入栈右边再入左边，保证左边先处理：

class Solution {
    public void flatten(TreeNode root) {
        helper(root);
    }

    private void helper(TreeNode root) {
        if (root == null) return;
        TreeNode last = new TreeNode(0, null, root);
        Deque<TreeNode> stack = new LinkedList<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode top = stack.poll();
            last.left = null;
            last.right = top;
            last = top;
            // 右边先入栈，保证左边先处理
            if (top.right != null) stack.push(top.right);
            if (top.left != null) stack.push(top.left);
        }
    }
}

迭代2

class Solution {
    public void flatten(TreeNode root) {
        helper(root);
    }

    // 先序遍历树的时候顺序是中左右
    // 如果一个节点的左子节点为空，则为 中、右 ，中的右边就是下一个节点
    // 如果一个节点的左子节点不为空，则为 中、左子节点的最右节点、右
    // 也就是说一个节点的左子节点不为空时，中的右边应该是左子节点的最右节点，然后再跟着右节点
    private void helper(TreeNode root) {
        while (root != null) {
            if (root.left != null) {
                TreeNode next = root.left;
                TreeNode pre = next;
                // 找左子节点的最右节点
                while (pre.right != null) {
                    pre = pre.right;
                }
                // 左子节点的最右节点的下一个为右节点
                pre.right = root.right;
                root.left = null;
                root.right = next;
            }
            root = root.right;
        }
    }
}

路径总和 III

二叉树的节点个数的范围是 [0,1000]
-10^9 <= Node.val <= 10^9
-1000 <= targetSum <= 1000

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

穷举 O(N^2)

访问每一个节点 node，检测以 node 为起始节点且向下延深的路径有多少种。我们递归遍历每一个节点的所有可能的路径，然后将这些路径数目加起来即为返回结果。

定义 helper(p, val) 表示以 p 为起点向下满足和为 val 的路径数目。对每个节点 p 求出 helper(p, targetSum) 就是答案。

helper 的实现为

private int helper(TreeNode root, long targetSum) {
    int ret = 0;
    if (root == null) return 0;
    if (root.val == targetSum) ret++;
    ret += helper(root.left, targetSum - root.val);
    ret += helper(root.right, targetSum - root.val);
    return ret;
}

接下来是对于每个节点都进行 helper，这里先 dfs 遍历所有节点，并对所有节点进行 helper 即可。

class Solution {
    public int pathSum(TreeNode root, long targetSum) {
        return dfs(root, targetSum);
    }

    // 计算所有节点的 helper
    private int dfs(TreeNode root, long targetSum) {
        if (root == null) return 0;
        int ret = 0;
        ret += helper(root, targetSum);
        ret += dfs(root.left, targetSum);
        ret += dfs(root.right, targetSum);
        return ret;
    }

    // 计算以 root 节点向下和为 val 的路径数目
    private int helper(TreeNode root, long targetSum) {
        int ret = 0;
        if (root == null) return 0;
        if (root.val == targetSum) ret++;
        ret += helper(root.left, targetSum - root.val);
        ret += helper(root.right, targetSum - root.val);
        return ret;
    }
}

前缀和优化 O(N)

我们定义节点的前缀和为：由根结点到当前结点的路径上所有节点的和。

我们利用先序遍历二叉树，记录下根节点 root 到当前节点 p 的路径上除当前节点以外所有节点的前缀和，在已保存的路径前缀和中查找是否存在前缀和刚好等于当前节点到根节点的前缀和 cur 减去 targetSum。

如果 (cur - targetSum) 存在，那么 cur - (cur - targetSum) = targetSum 也存在，就是从某个路径到当前节点的和为 targetSum。

key保存前缀和，value保存对应此前缀和的数量。

然后总体的思路和 560 是一样的。

class Solution {
    public int pathSum(TreeNode root, int targetSum) {
        Map<Long, Integer> prefix = new HashMap<Long, Integer>();
        prefix.put(0L, 1);
        return dfs(root, prefix, 0L, targetSum);
    }

    private int dfs(TreeNode root, Map<Long, Integer> prefix, long cur, int targetSum) {
        if (root == null) return 0;
        int ret = 0;
        // 前缀和
        cur += root.val;

        // 当前从根节点 root 到节点 node 的前缀和为 cur
        // 两节点间的路径和 = 两节点的前缀和之差
        // 查找是否存在 cur - targetSum 的前缀和
        // 如果该前缀和存在，那么 cur - (cur - targetSum) = targetSum 存在
        // 也就是说

        ret = prefix.getOrDefault(cur - targetSum, 0);
        prefix.put(cur, prefix.getOrDefault(cur, 0) + 1);
        ret += dfs(root.left, prefix, cur, targetSum);
        ret += dfs(root.right, prefix, cur, targetSum);
        prefix.put(cur, prefix.getOrDefault(cur, 0) - 1);

        return ret;
    }
}

二叉树的最近公共祖先

暴力递归做法

每个节点判断是不是子节点是不是同时包含 p 和 q

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return dfs(root, p, q);
    }

    // 遍历每个节点，当节点的子树同时包含 p 和 q 时，该节点为最近公共祖先
    private TreeNode dfs(TreeNode root, TreeNode p, TreeNode q) {
        if (root == p || root == q) return root;
        if (check(root.left, p, q) && check(root.right, p, q)) return root;
        if (check(root.right, p, q) == false) return dfs(root.left, p, q);
        return dfs(root.right, p, q);
    }

    // root 开始遍历的所有节点中是否有 p 或者 q
    private boolean check(TreeNode root, TreeNode p, TreeNode q) {
        // 如果 p，q 的公共节点为 root，那么从 root 能遍历得到 p 和 q
        if (root == null) return false;
        if (root == p || root == q) return true;
        return check(root.left, p, q) || check(root.right, p, q);
    }
}

改进递归做法

如果要找的节点只在左子树中，那么最近公共祖先也只在左子树中。
如果要找的节点只在右子树中，那么最近公共祖先也只在右子树中。
如果要找的节点左右子树都有，那么最近公共祖先就是当前节点。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return dfs(root, p, q);
    }

    // 对于 root 找 p 和 q
    private TreeNode dfs(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) return null;
        if (root == p || root == q) return root;

        TreeNode left = dfs(root.left, p, q);
        TreeNode right = dfs(root.right, p, q);
        if (left == null) return right; // 如果要找的节点只在右子树中，那么最近公共祖先也只在右子树中
        if (right == null) return left; // 如果要找的节点只在左子树中，那么最近公共祖先也只在左子树中
        // 如果要找的节点左右子树都有，那么最近公共祖先就是当前节点
        if (left != null && right != null) return root;
        return null;
    }
    
}

记录父节点的做法

用哈希表记录每个 TreeNode 的父节点，然后遍历 p 的父节点和 q 的父节点，最先出现的那个就是最近公共祖先

class Solution {
    private HashMap<TreeNode, TreeNode> map = new HashMap<>();
    private Set<TreeNode> set = new HashSet<>();

    private void dfs(TreeNode root) {
        if (root == null) return;
        if (root.left != null) {
            map.put(root.left, root);
            dfs(root.left);
        }
        if (root.right != null) {
            map.put(root.right, root);
            dfs(root.right);
        }
    }

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        dfs(root);
        while(p != null) {
            set.add(p); // 要在 get 之前，这样能够处理一个 p 是 q 的父节点的情况
            p = map.get(p);
        }

        while (q != null) {
            if (set.contains(q)) return q;
            q = map.get(q);
        }

        return null;
    }
}

二叉树中的最大路径和

与二叉树最大直径有异曲同工之妙。

class Solution {
    private int ans = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        helper(root);
        return ans;
    }

    private int helper(TreeNode root) {
        if (root == null) return 0;
        int leftMax = Math.max(helper(root.left), 0);
        int rightMax = Math.max(helper(root.right), 0);
        ans = Math.max(leftMax + rightMax + root.val, ans);
        return root.val + Math.max(leftMax, rightMax);
    }
}

最深叶节点的最近公共祖先

暴力递归

先找到最深叶节点，然后找最近公共祖先

class Solution {
    Map<Integer, List<TreeNode>> deepMap = new HashMap<>();

    public TreeNode lcaDeepestLeaves(TreeNode root) {
        // 先找到最深叶节点，然后找最近公共祖先
        deepestNodes(root, 0);
        List<TreeNode> deepestNodes = null;
        int deep = 0;
        for (Map.Entry<Integer, List<TreeNode>> entry : deepMap.entrySet()) {
            if (entry.getKey() >= deep) {
                deepestNodes = entry.getValue();
            }
        }
        // 两两找最近公共祖先
        return MergeLCA(root, deepestNodes, 0, deepestNodes.size() - 1);

        // 数组找最近公共祖先
        // return ArrayLCA(root, deepestNodes);
    }

    private TreeNode ArrayLCA(TreeNode root, List<TreeNode> list) {
        TreeNode ans = list.get(0);
        for (int i = 1; i < list.size(); i++) {
            ans = LCA(root, ans, list.get(i));
        }
        return ans;
    }

    private TreeNode MergeLCA(TreeNode root, List<TreeNode> list, int left, int right) {
        if (right - left == 0) return list.get(left);
        if (right - left == 1) {
            return LCA(root, list.get(left), list.get(right));
        }
        if (right - left > 1) {
            int mid = left + (right - left) / 2;
            return LCA(root, MergeLCA(root, list, left, mid - 1), MergeLCA(root, list, mid + 1, right));
        }
        return null;
    }

    private void deepestNodes(TreeNode root, int deep) {
        if (root == null) return;
        List<TreeNode> nodes = deepMap.getOrDefault(deep, new ArrayList<>());
        nodes.add(root);
        deepMap.put(deep, nodes);
        deepestNodes(root.left, deep + 1);
        deepestNodes(root.right, deep + 1);
    }

    private TreeNode LCA(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) return null;
        if (root == p || root == q) return root;
        TreeNode left = LCA(root.left, p, q);
        TreeNode right = LCA(root.right, p, q);
        if (left == null) return right; // 左子树中没有 LCA
        if (right == null) return left; // 右子树中没有 LCA
        if (left != null && right != null) return root;
        return null;
    }
}

改进的递归

从根节点开始递归，同时维护全局最大深度 deepMax。
在「递」的时候往下传 depth，用来表示当前节点的深度。
在「归」的时候往上传当前子树最深的空节点的深度。这里为了方便，用空节点代替叶子，因为最深的空节点的上面一定是最深的叶子。
设左子树最深空节点的深度为 leftMax，右子树最深空节点的深度为 rightMax。如果最深的空节点左右子树都有，也就是 leftMax=rightMax=deepMax，那么更新答案为当前节点。注意这并不代表我们找到了答案，如果后面发现了更深的空节点，答案还会更新。另外注意，这个判断方式在只有一个最深叶子的情况下，也是正确的。

class Solution {
    int deepMax = 0;
    TreeNode ans = null;

    public TreeNode lcaDeepestLeaves(TreeNode root) {
        dfs(root, 0);
        return ans;
    }

    private int dfs(TreeNode root, int deep) {
        if (root == null) {
            deepMax = Math.max(deepMax, deep);
            return deep;
        }
        // 递
        int leftMax = dfs(root.left, deep + 1);
        int rightMax = dfs(root.right, deep + 1);
        // 归
        if (leftMax == deepMax && rightMax == deepMax) { // 最深节点在左右节点都有，只关心：当前节点的左右子树是否都达到了最深深度
            ans = root;
        }
        return Math.max(leftMax, rightMax);
    }

}

图论

岛屿数量

class Solution {
    private int count = 0;
    private boolean[][] visited;
    private int[][] dirs = {
        {0, 1},
        {0, -1},
        {1, 0},
        {-1, 0}
    };

    public int numIslands(char[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        visited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (!visited[i][j] && grid[i][j] == '1') {
                    dfs(grid, i, j);
                    count++;
                }
            }
        }
        return count;
    }

    // 访问所有相邻的岛屿
    // x是行，y是列
    private void dfs(char[][] grid, int x, int y) {    
        visited[x][y] = true;
        for (int i = 0; i < 4; i++) { // 访问所有相邻的
            int dirX = dirs[i][0], dirY = dirs[i][1];
            int m = grid.length;
            int n = grid[0].length;
            int newX = x + dirX, newY = y + dirY;
            if (newX >= 0 && newX < m && newY >= 0 && newY < n && !visited[newX][newY] && grid[newX][newY] == '1') {
                visited[newX][newY] = true; // 原有的连通岛屿都设置成已经访问
                dfs(grid, newX, newY);
            }
        }
    }
}

腐烂的橘子

单源 bfs

不要改动橘子矩阵，新增一个时间矩阵表示橘子的情况。

bfs，如果时间更小则更新时间矩阵。

这个是单源 bfs，需要对于每个腐烂的橘子都进行 bfs。

class Solution {
    private boolean[][] visited;
    private int[][] dirs = {
        {-1, 0},
        {1, 0},
        {0, 1},
        {0, -1},
    }, allTime;
    private int m, n;

    public int orangesRotting(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        visited = new boolean[m][n];
        allTime = new int[m][n];
        for (int[] row : allTime) {
            Arrays.fill(row, 0x3f3f3f3f);
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                bfs(grid, i, j);
            }
        }
        int maxTime = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] != 0 && allTime[i][j] == 0x3f3f3f3f) { // 存在没腐烂的橘子
                    return -1;
                } else if (grid[i][j] > 0 && allTime[i][j] != 0x3f3f3f3f) {
                    maxTime = Math.max(allTime[i][j], maxTime);
                }
            }
        }
        return maxTime;
    }

    // 返回当前橘子开始最多要多少时间感染所有可感染的橘子
    private void bfs(int[][] grid, int row, int col) {
        if (grid[row][col] != 2) return; // 不是腐烂橘子就不能继续传染
        Queue<int[]> queue = new LinkedList<>();
        queue.offer(new int[]{row, col, 0});
        allTime[row][col] = 0;
        visited[row][col] = true;
        while (!queue.isEmpty()) {
            int[] pos = queue.poll();
            for (int i = 0; i < 4; i++) {
                if (pos[2] == 0x3f3f3f3f) continue; // 不是腐烂橘子就不能继续传染
                int newRow = dirs[i][0] + pos[0];
                int newCol = dirs[i][1] + pos[1];
                int newTime = 1 + pos[2];
                if (ok(newRow, newCol, newTime) && grid[newRow][newCol] > 0) {
                    queue.offer(new int[]{newRow, newCol, newTime});
                    visited[newRow][newCol] = true;
                    allTime[newRow][newCol] = newTime;
                    // grad[newRow][newCol] = 2;
                }
            }
        }
    }

    private boolean ok(int row, int col, int time) {
        return row >= 0 && row < m && col >= 0 && col < n && (!visited[row][col] || time < allTime[row][col]);
    }
}

多源 bfs

把所有腐烂的橘子都放到队列里面，进行多源 bfs，这样就不用每个腐烂橘子都 bfs 了。

class Solution {
    private boolean[][] visited;
    private int[][] dirs = {
        {-1, 0},
        {1, 0},
        {0, 1},
        {0, -1},
    }, allTime;
    private int m, n;
    Queue<int[]> queue = new LinkedList<>();

    public int orangesRotting(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        visited = new boolean[m][n];
        allTime = new int[m][n];
        for (int[] row : allTime) {
            Arrays.fill(row, 0x3f3f3f3f);
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 2) {
                    queue.offer(new int[]{i, j, 0});
                    allTime[i][j] = 0;
                    visited[i][j] = true;
                }
            }
        }

        bfs(grid);

        int maxTime = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] != 0 && allTime[i][j] == 0x3f3f3f3f) { // 存在没腐烂的橘子
                    return -1;
                } else if (grid[i][j] > 0 && allTime[i][j] != 0x3f3f3f3f) {
                    maxTime = Math.max(allTime[i][j], maxTime);
                }
            }
        }
        return maxTime;
    }

    // 返回当前橘子开始最多要多少时间感染所有可感染的橘子
    private void bfs(int[][] grid) {
        while (!queue.isEmpty()) {
            int[] pos = queue.poll();
            for (int i = 0; i < 4; i++) {
                int newRow = dirs[i][0] + pos[0];
                int newCol = dirs[i][1] + pos[1];
                int newTime = 1 + pos[2];
                if (ok(newRow, newCol, newTime) && grid[newRow][newCol] > 0) {
                    queue.offer(new int[]{newRow, newCol, newTime});
                    visited[newRow][newCol] = true;
                    allTime[newRow][newCol] = newTime;
                }
            }
        }
    }

    private boolean ok(int row, int col, int time) {
        return row >= 0 && row < m && col >= 0 && col < n && (!visited[row][col] || time < allTime[row][col]);
    }
}

Trie 树

HashMap 实现

class Trie {
    Map<String, Boolean> map = new HashMap<>();
    Map<String, Boolean> prefixMap = new HashMap<>();

    public Trie() {
        
    }
    
    public void insert(String word) {
        for (int i = 1; i <= word.length(); i++) {
            prefixMap.put(word.substring(0, i), true);
        }
        map.put(word, true);
    }
    
    public boolean search(String word) {
        return map.containsKey(word);
    }
    
    public boolean startsWith(String prefix) {
        return prefixMap.containsKey(prefix);
    }
}

正常实现

class Trie {
    class TrieNode {
        Map<Character, TrieNode> children = new HashMap<>();
        boolean isEnd = false;
        public TrieNode() {
            
        }
    }

    TrieNode root;
    public Trie() {
        root = new TrieNode();
    }
    
    public void insert(String word) {
        TrieNode node = root;
        for (char ch : word.toCharArray()) {
            node = node.children.computeIfAbsent(ch, v -> new TrieNode());
        }
        node.isEnd = true;
    }
    
    public boolean search(String word) {
        TrieNode node = root;
        for (char ch : word.toCharArray()) {
            node = node.children.get(ch);
            if (node == null) return false;
        }
        return node.isEnd;
    }
    
    public boolean startsWith(String prefix) {
        TrieNode node = root;
        for (char ch : prefix.toCharArray()) {
            node = node.children.get(ch);
            if (node == null) return false;
        }
        return true;
    }
}

课程表

1 <= numCourses <= 2000
0 <= prerequisites.length <= 5000

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

像是要检测并完成图中是否有环？

拓扑排序的经典题？

我们将每一门课看成一个节点；

如果想要学习课程A之前必须完成课程B，那么我们从B到A连接一条有向边。这样以来，在拓扑排序中，B一定出现在A的前面。

求出该图是否存在拓扑排序，就可以判断是否有一种符合要求的课程学习顺序。事实上，由于求出一种拓扑排序方法的最优时间复杂度为O(n+m)，其中n和m分别是有向图G的节点数和边数，方法见210. 课程表 II 的官方题解。而判断图G是否存在拓扑排序，至少也要对其进行一次完整的遍历，时间复杂度也为O(n+m)。因此不可能存在一种仅判断图是否存在拓扑排序的方法，它的时间复杂度在渐进意义上严格优于O(n+m)。这样一来，我们使用和210. 课程表 II完全相同的方法，但无需使用数据结构记录实际的拓扑排序。为了叙述的完整性，下面的两种方法与210. 课程表 II 的官方题解完全相同，但在「算法」部分后的「优化」部分说明了如何省去对应的数据结构。

代码与下面的 课程表 II 相同，如果存在拓扑排序就是 true。

课程表 II

BFS

拓扑排序，bfs 思路，找入度为 0 的节点，放到队列和 ans 里面，并把 uv 的 v 节点的入度减一，并检测有哪些节点的入度为 0，继续放入队列中。

class Solution {
    List<List<Integer>> edges; // 有向图
    int[] indeg;
    int[] ans;
    int index = 0;
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        edges = new ArrayList<>();
        ans = new int[numCourses];
        indeg = new int[numCourses]; // 节点的入度
        Queue<Integer> queue = new LinkedList<>();

        for (int i = 0; i < numCourses; i++) {
            edges.add(new ArrayList<Integer>());
        }
        for (int[] req : prerequisites) {
            edges.get(req[1]).add(req[0]);
            indeg[req[0]]++;
        }
        for (int i = 0; i < numCourses; i++) {
            if (indeg[i] == 0) {
                queue.offer(i);
            }
        }
        while (!queue.isEmpty()) {
            int first = queue.poll();
            ans[index++] = first;
            List<Integer> v = edges.get(first);
            for (int i = 0; i < v.size(); i++) {
                indeg[v.get(i)]--;
                if (indeg[v.get(i)] == 0) {
                    queue.offer(v.get(i));
                }
            }
        }
        if (index < numCourses) return new int[0];
        else return ans;
    }
}

回溯

回溯法就是暴力搜索，并不是什么高效的算法，最多再剪枝一下。

回溯算法能解决如下问题：

组合问题：N个数里面按一定规则找出k个数的集合
排列问题：N个数按一定规则全排列，有几种排列方式
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
棋盘问题：N皇后，解数独等等

模板框架：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

全排列

主要就是回溯前后的状态的更新和恢复

还有要想清楚选定了某个元素之后，剩余的选择的范围是哪些。

对于全排列来说是选定了元素之后，这个元素不能再选。

class Solution {
    private int n;
    private boolean[] visited;
    private List<List<Integer>> ans;
    private List<Integer> tmp;

    public List<List<Integer>> permute(int[] nums) {
        n = nums.length;
        visited = new boolean[n];
        ans = new ArrayList<>();
        tmp = new ArrayList<>();
        dfs(nums, 0);
        return ans;
    }

    private void dfs(int[] nums, int times) {
        if (times == n) {
            ans.add(new ArrayList<>(tmp));
            return;
        }
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                tmp.add(nums[i]);
                visited[i] = true;
                dfs(nums, times + 1);
                visited[i] = false;
                tmp.remove(tmp.size() - 1);
            }
        }
    }
}

子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

1 2	`输入：nums = [1,2,3] 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]`

DFS

要点在于思考选择了第一个元素，比如 [1] 之后，后续的选择就不能再选 1 了。

选了 [1, 2] 就不能有 [2, 1] 了。所以要点在于选元素的时候，候选项是下标大于自己的元素里面。

所以注意 dfs 的第二个参数是 start + 1 而不是 i + 1。

class Solution {
    private List<List<Integer>> ans = new ArrayList<>();
    private boolean[] visited;
    List<Integer> tmp = new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
        int n = nums.length;
        visited = new boolean[n];
        dfs(nums, 0);
        return ans;
    }

    // start 定义候选项的开始下标
    private void dfs(int[] nums, int start) {
        ans.add(new ArrayList<>(tmp));
        for (int i = start; i < nums.length; i++) {
            if (!visited[i]) {
                tmp.add(nums[i]);
                visited[i] = true;
                dfs(nums, start + 1);
                visited[i] = false;
                tmp.remove(tmp.size() - 1);
            }
        }
    }

}

位操作

例如，n=3，a={5,2,9}时：

0/1序列子集 0/1序列对应的二进制数
000 {} 0
001 {9} 1
010 {2} 2
011 {2,9} 3
100 {5} 4
101 {5,9} 5
110 {5,2} 6
111 {5,2,9} 7

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        int n = nums.length;
        List<List<Integer>> ans = new ArrayList<>();
        for (int i = 0; i < (1 << n); i++) {
            List<Integer> tmp = new ArrayList<>();
            for (int j = 0; j < n; j++) {
                if ((i & (1 << j)) != 0) {
                    tmp.add(nums[j]);
                }
            }
            ans.add(tmp);
        }
        return ans;
    }
}

电话号码的数字组合

迭代

for 套 for，第一个 for 找上一层的号码，第二个 for 根据上一层加新的号码

class Solution {
    Map<Character, char[]> map = new HashMap<>();
    List<List<String>> ans = new ArrayList<>();

    public List<String> letterCombinations(String digits) {
        if (digits.length() == 0) return new ArrayList<String>();
        map.put('2', new char[]{'a', 'b', 'c'});
        map.put('3', new char[]{'d', 'e', 'f'});
        map.put('4', new char[]{'g', 'h', 'i'});
        map.put('5', new char[]{'j', 'k', 'l'});
        map.put('6', new char[]{'m', 'n', 'o'});
        map.put('7', new char[]{'p', 'q', 'r', 's'});
        map.put('8', new char[]{'t', 'u', 'v'});
        map.put('9', new char[]{'w', 'x', 'y', 'z'});

        for (int digitsIndex = 0; digitsIndex < digits.length(); digitsIndex++) {
            char[] res = map.get(digits.charAt(digitsIndex));
            List<String> tmp;
            if (digitsIndex == 0) {
                tmp = new ArrayList<>();
                for (char c : res) {
                    tmp.add(String.valueOf(c));
                }
                ans.add(tmp);
            } else {
                List<String> old = ans.get(digitsIndex - 1);
                tmp = new ArrayList<>();
                int size = old.size();
                for (char c : res) {
                    for (int i = 0 ; i < size; i++) {
                        tmp.add(old.get(i) + c);
                    }
                }
                ans.add(tmp);
            }
        }
        return ans.get(ans.size() - 1);
    }

}

递归

要点在于转换为子问题，只需要上一层的状态即可。要点在于 dfs(i) 表示第 i 个字母对应的答案。

class Solution {
    Map<Character, char[]> map = new HashMap<>();
    List<List<String>> ans = new ArrayList<>();

    public List<String> letterCombinations(String digits) {
        if (digits.length() == 0) return new ArrayList<String>();
        map.put('2', new char[]{'a', 'b', 'c'});
        map.put('3', new char[]{'d', 'e', 'f'});
        map.put('4', new char[]{'g', 'h', 'i'});
        map.put('5', new char[]{'j', 'k', 'l'});
        map.put('6', new char[]{'m', 'n', 'o'});
        map.put('7', new char[]{'p', 'q', 'r', 's'});
        map.put('8', new char[]{'t', 'u', 'v'});
        map.put('9', new char[]{'w', 'x', 'y', 'z'});

        return dfs(digits, new ArrayList<String>(), 0);
    }

    private List<String> dfs(String digits, List<String> lastAns, int times) {
        if (times < digits.length()) {
            List<String> ans = new ArrayList<>();
            char[] chars = map.get(digits.charAt(times));
            if (lastAns.size() != 0) {
                for (int i = 0; i < lastAns.size(); i++) {
                    for (char ch : chars) {
                        ans.add(lastAns.get(i) + ch);
                    }
                }
            } else {
                for (char ch : chars) {
                    ans.add("" + ch);
                }
            }

            return dfs(digits, ans, times + 1);
        } else {
            return lastAns;
        }
    }

}

组合总数

要点：

ans.add(new ArrayList<>(tmp)); 添加的是 tmp 的 clone。
dfs(candidates, target - num, i); 第三个参数是 i ，而不是 start + 1，既可以保证选到相同的数字，又保证没有同一种的不同组合。比如 [3, 5] 和 [5, 3]。

class Solution {
    private List<List<Integer>> ans = new ArrayList<>();
    private List<Integer> tmp = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        dfs(candidates, target, 0);
        return ans;
    }

    private void dfs(int[] candidates, int target, int start) {
        if (target < 0) return;
        if (target == 0) {
            ans.add(new ArrayList<>(tmp));
            return;
        }
        for (int i = start; i < candidates.length; i++) {
            int num = candidates[i];
            tmp.add(num);
            dfs(candidates, target - num, i);
            tmp.remove(tmp.size() - 1);
        }
    }
}

括号生成

要点：

候选为 ( 和 )，候选的个数为 n。每次应该可以从候选中任意选择。
选择之后添加到 tmp，然后继续递归，之后要删除 tmp 中添加的内容。
right 要在 left 之后才能被选择，所以放 right 的时候要确认可以选的 right > left。

class Solution {
    private List<String> ans = new ArrayList<>();
    private StringBuilder sb = new StringBuilder();

    public List<String> generateParenthesis(int n) {
        dfs(n, n);
        return ans;
    }

    // 候选者有 n 个左括号，n 个右括号
    private void dfs(int left, int right) {
        if (left == 0 && right == 0) {
            ans.add(sb.toString());
            return;
        }

        if (left > 0) {
            sb.append('(');
            dfs(left - 1, right);
            sb.delete(sb.length() - 1, sb.length());
        }

        if (right > 0 && right > left) {
            sb.append(')');
            dfs(left, right - 1);
            sb.delete(sb.length() - 1, sb.length());
        }
    }
}

单词搜索

要点：

不允许重复使用，所以要使用 visited 数组。
回溯记得设置 visited 为 false。

class Solution {
    private int m, n;
    private boolean[][] visited;
    private int[][] dirs = new int[][]{
        {-1, 0},
        {1, 0},
        {0, 1},
        {0, -1}
    };
    public boolean exist(char[][] board, String word) {
        m = board.length;
        n = board[0].length;
        visited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == word.charAt(0)) {
                    if (1 == word.length()) return true;
                    visited[i][j] = true;
                    if (dfs(board, word, 1, i, j)) return true;
                    visited[i][j] = false;
                }
            }
        }
        return false;
    }

    private boolean dfs(char[][] board, String word, int start, int row, int col) {
        for (int i = 0; i < 4; i++) {
            int[] dir = dirs[i];
            int newRow = row + dir[0];
            int newCol = col + dir[1];
            if (check(board, newRow, newCol, word.charAt(start))) { // 继续搜索可能找到的情况
                if (start == word.length() - 1) return true; // 找到了最后一个字母
                visited[newRow][newCol] = true;
                boolean res = dfs(board, word, start + 1, newRow, newCol);
                visited[newRow][newCol] = false;
                if (res) return true;
            }
        }
        return false;
    }

    private boolean check(char[][] board, int row, int col, char need) {
        return row >= 0 && row < m && col >= 0 && col < n && !visited[row][col] && need == board[row][col];
    }
}

分割回文串

要点：

不管是递归还是 dp，重要的都是划分子问题，用 dp[i][j] 表示。
这里是枚举所有的分割方法，然后判断是不是回文字符串。枚举可以用回溯法，判断可以使用 dp 等方法进行优化。
枚举要有条理的枚举，比如从 i 开始，一直枚举到结尾，然后下次从 i + 1 再到结尾。

数据很弱，直接回溯都能过。

直接回溯

class Solution {
    List<List<String>> ans = new ArrayList<>();
    List<String> tmp = new ArrayList<>();
    int n;

    public List<List<String>> partition(String s) {
        n = s.length();
        dfs(s, 0);
        return ans;
    }

    private void dfs(String s, int start) {
        if (start == n) {
            ans.add(new ArrayList<>(tmp));
            return;
        }

        for (int i = start + 1; i <= n; i++) {
            String sub = s.substring(start, i);
            if (check(sub)) { // 当前分割方法是回文串
                tmp.add(sub);
                dfs(s, i); // 左闭右开，继续进行分割
                tmp.remove(tmp.size() - 1);
            }
        }
    }

    private boolean check(String s) {
        int left = 0, right = s.length() - 1;
        while (left < right) {
            if (s.charAt(left) != s.charAt(right)) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
}

回溯 + dp

其实就是用 dp 记录一下哪些情况是回文字符串，这样就不用重复判断了。

class Solution {
    List<List<String>> ans = new ArrayList<>();
    List<String> tmp = new ArrayList<>();
    boolean[][] dp;
    int n;

    public List<List<String>> partition(String s) {
        n = s.length();
        initDp(s);
        dfs(s, 0);
        return ans;
    }

    private void initDp(String s) {
        dp = new boolean[n + 1][n + 1]; // 左闭右闭
        for (int i = 0; i < n; i++) {
            dp[i][i] = true; // 单字符为回文串
        }
        for (int i = 0; i < n - 1; i++) {
            if (s.charAt(i) == s.charAt(i + 1)) {
                dp[i][i + 1] = true; // 双字符为回文串
            }
        }
        for (int i = n - 2; i >= 0; i--) {
            for (int j = i + 1; j < n; j++) {
                if (dp[i + 1][j - 1] && s.charAt(i) == s.charAt(j))
                dp[i][j] = true;
            }
        }
    }

    private void dfs(String s, int start) {
        if (start == n) {
            ans.add(new ArrayList<>(tmp));
            return;
        }

        for (int i = start + 1; i <= n; i++) {
            String sub = s.substring(start, i);
            if (dpCheck(start, i - 1)) { // 当前分割方法是回文串
                tmp.add(sub);
                dfs(s, i); // 左闭右开，继续进行分割
                tmp.remove(tmp.size() - 1);
            }
        }
    }

    private boolean dpCheck(int start, int end) {
        return dp[start][end];
    }

    private boolean check(String s) {
        int left = 0, right = s.length() - 1;
        while (left < right) {
            if (s.charAt(left) != s.charAt(right)) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
}

记忆化递归

class Solution {
    List<List<String>> ans = new ArrayList<>();
    List<String> tmp = new ArrayList<>();
    int[][] dp;
    int n;

    public List<List<String>> partition(String s) {
        n = s.length();
        dp = new int[n][n];
        dfs(s, 0);
        return ans;
    }

    private void dfs(String s, int start) {
        if (start == n) {
            ans.add(new ArrayList<>(tmp));
            return;
        }

        for (int i = start + 1; i <= n; i++) {
            String sub = s.substring(start, i);
            if (memoryCheck(s, start, i - 1) == 1) { // 当前分割方法是回文串
                tmp.add(sub);
                dfs(s, i); // 左闭右开，继续进行分割
                tmp.remove(tmp.size() - 1);
            }
        }
    }

    private int memoryCheck(String s, int i, int j) {
        if (dp[i][j] != 0) return dp[i][j]; // 记忆命中
        if (i >= j) dp[i][j] = 1;
        else if (s.charAt(i) == s.charAt(j)) {
            dp[i][j] = memoryCheck(s, i + 1, j - 1);
        } else {
            dp[i][j] = -1;
        }
        return dp[i][j];
    }

    private boolean check(String s) {
        int left = 0, right = s.length() - 1;
        while (left < right) {
            if (s.charAt(left) != s.charAt(right)) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
}

二分查找

搜索插入位置

左闭右闭

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        int mid = 0;
        while (left <= right) {
            mid = left + (right - left) / 2;
            if (nums[mid] == target) return mid;
            else if (nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

左闭右开

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0;
        int right = nums.length;
        int mid = 0;
        while (left < right) {
            mid = left + (right - left) / 2;
            if (nums[mid] == target) return mid;
            else if (nums[mid] > target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

搜索二维矩阵

先在所有行中二分搜索第一个元素，然后在确定的某一行中搜索。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int left = 0;
        int right = matrix.length;
        int mid = 0;

        // 先二分行
        while (left < right) {
            mid = left + (right - left) / 2;
            if (matrix[mid][0] == target) {
                return true;
            } else if (matrix[mid][0] > target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }

        int row = 0;
        if (left > 0) row = left - 1;
        else row = left;
        left = 0;
        right = matrix[0].length;
        // 再二分列
        while (left < right) {
            mid = left + (right - left) / 2;
            if (matrix[row][mid] == target) return true;
            else if (matrix[row][mid] > target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return false;
    }

}

在排序数组中查找元素的第一个和最后一个位置

一个搜索 lower bound，另一个 upper bound，搜索 lower bound 是等于 target 的时候设置 ans[0] = mid 并且 right = mid；upper bound 是等于 target 的时候设置ans[1] = mid 并且 left = mid + 1。

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int left = 0;
        int right = nums.length;
        int mid;
        int[] ans = new int[]{-1, -1};

        // lower bound
        while (left < right) {
            mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                ans[0] = mid;
                right = mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }

        // upper bound
        left = 0;
        right = nums.length;
        while (left < right) {
            mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                ans[1] = mid;
                left = mid + 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return ans;
    }
}

搜索旋转排序数组

对一个旋转后的数组进行切分，总会切分成两部分，两部分中必定有一部分是顺序的，另一部分是乱序的，对于顺序的进行二分搜索，对于乱序的继续切分。

然后还要注意，判断在顺序部分的时候，nums[left] 和 target 的比较得是 <= ，否则无法处理 nums = [1, 3], target = 1 的情况。

class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length;
        int mid;
        while (left < right) {
            mid = left + (right - left) / 2;
            if (nums[mid] == target) return mid;
            if (nums[left] < nums[mid]) { // 左边顺序，右边乱序
                if (nums[left] <= target && target < nums[mid]) { // target 在左面顺序部分
                    right = mid;
                } else { // target 在乱序部分
                    left = mid + 1;
                }
            } else { // 右边顺序，左边乱序
                if (nums[mid] < target && target <= nums[right - 1]) { // target 在右面顺序部分
                    left = mid + 1;
                } else {
                    right = mid;
                }
            }
        }
        return -1;
    }
}

寻找旋转排序数组中的最小值

搜索旋转排序数组的简化版本，无论在哪里分隔，都是有序和无序部分，有序部分取最小值，然后继续去无序部分继续搜索。

class Solution {
    public int findMin(int[] nums) {
        int left = 0;
        int right = nums.length;
        int mid;
        int min = nums[0];
        while (left < right) {
            mid = left + (right - left) / 2;
            // nums[left] ... mid ... nums[right]
            if (nums[left] < nums[mid]) { // 左边有序
                min = Math.min(min, nums[left]);
                left = mid + 1;
            } else { // 右边有序
                min = Math.min(min, nums[mid]);
                right = mid;
            }
        }
        return min;
    }
}

寻找两个正序数组的中位数

这道题的关键在于对中位数的理解，一个数组的中位数是能够将数组分为两部分的数，且左边部分的最大值小于右边部分最小值。

对于两个数组的情况：

image-20250227154454826

第一个条件：左边元素个数和右边相等或左边多一个

然后分割线左边元素个数和右边元素个数是可以被计算的，假设长度为 m 和 n，当 m + n 为偶数时，左边元素个数 = 右边元素个数 = (m + n) / 2。

当 m + n 为奇数时，假设中位数在左边，于是左边元素个数 = (m + n + 1) / 2。

又偶数的时候，(m + n + 1) / 2 = (m + n) / 2，因为默认是向下取整。所以统一成了左边元素个数 = (m + n + 1) / 2。

第二个条件：分割线左边最大元素 <= 分割线右边最大元素

对于两个数组的情况下：

第一个数组的分割线左边最大值 <= 第二个数组的分割线右边最小值
第二个数组的分割线左边最大值 <= 第一个数组的分割线右边最小值

如果不满足上面的情况，就要进行调整。

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        if (nums1.length > nums2.length) return findMedianSortedArrays(nums2, nums1);
        int m = nums1.length, n = nums2.length;
        int left = 0, right = m;
        // median1: 前一部分最大值
        // median2: 后一部分最小值
        int median1 = 0, median2 = 0;
        while (left <= right) {
            // 分割线在第 1 个数组右边的第 1 个元素的下标 i = 分割线在第 1 个数组左边的元素个数
            int i = left + (right - left) / 2;
            // 分割线在第 2 个数组右边的第 1 个元素的小标 j = 分割线在第 2 个数组左边的元素的个数
            // 也就是左边的部分还需要的元素的个数，根据 i 的位置，j 的位置根据数量就唯一确定了。
            int j = (m + n + 1) / 2 - i;

            int nums_i_minus_1 = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]);
            int nums_i_add_1 = (i == m ? Integer.MAX_VALUE : nums1[i]); // 分割线右边第一个元素
            int nums_j_minus_1 = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]);
            int nums_j_add_1 = (j == n ? Integer.MAX_VALUE : nums2[j]); // 分割线右边第一个元素

            // if (median1 > median2) {
            if (nums_i_minus_1 > nums_j_add_1) {
                right = i - 1;
            } else {
                median1 = Math.max(nums_i_minus_1, nums_j_minus_1);
                median2 = Math.min(nums_i_add_1, nums_j_add_1);
                left = i + 1;
            }
        }

        return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;
    }
}

统计公平数对的数目

给你一个下标从 0 开始、长度为 n 的整数数组 nums ，和两个整数 lower 和 upper ，返回 公平数对的数目 。

如果 (i, j) 数对满足以下情况，则认为它是一个 公平数对 ：

0 <= i < j < n，且
lower <= nums[i] + nums[j] <= upper

由于排序不影响答案，可以先（从小到大）排序，这样可以二分查找。

nums 是 [1,2] 还是 [2,1]，算出来的答案都是一样的，因为加法满足交换律 $a + b = b + a$。

排序后，枚举右边的 nums[j]，那么左边的 nums[i] 需要满足 $0 \leq i < j$ 以及

$lower - nums[j] \leq nums[i] \leq upper - nums[j]$

计算 $\leq upper - nums[j]$ 的元素个数，减去 $< lower - nums[j]$ 的元素个数，即为满足上式的元素个数。(联想一下前缀和)

由于 nums 是有序的，我们可以在 $[0, j - 1]$ 中二分查找，原理见【基础算法精讲 04】：

找到 $> upper - nums[j]$ 的第一个数，设其下标为 $r$，那么下标在 $[0, r - 1]$ 中的数都是 $\leq upper - nums[j]$ 的，这有 $r$ 个。如果 $[0, j - 1]$ 中没有找到这样的数，那么二分结果为 $j$。这意味着 $[0, j - 1]$ 中的数都是 $\leq upper - nums[j]$ 的，这有 $j$ 个。
找到 $\geq lower - nums[j]$ 的第一个数，设其下标为 $l$，那么下标在 $[0, l - 1]$ 中的数都是 $< lower - nums[j]$ 的，这有 $l$ 个。如果 $[0, j - 1]$ 中没有找到这样的数，那么二分结果为 $j$。这意味着 $[0, j - 1]$ 中的数都是 $< lower - nums[j]$ 的，这有 $j$ 个。
满足 $lower - nums[j] \leq nums[i] \leq upper - nums[j]$ 的 nums[i] 的个数为 $r - l$，加入答案。

class Solution {
    public long countFairPairs(int[] nums, int lower, int upper) {
        Arrays.sort(nums);
        long ans = 0;
        for (int j = 0; j < nums.length; j++) {
            // 注意要在 [0, j-1] 中二分，因为题目要求两个下标 i < j
            int r = lowerBound(nums, j, upper - nums[j] + 1);
            int l = lowerBound(nums, j, lower - nums[j]);
            ans += r - l;
        }
        return ans;
    }

    private int lowerBound(int[] nums, int right, int target) {
        int left = -1;
        while (left + 1 < right) {
            int mid = (left + right) >>> 1;
            if (nums[mid] >= target) {
                right = mid;
            } else {
                left = mid;
            }
        }
        return right;
    }
}

栈

有效的括号

判断右括号的时候栈顶能不能匹配就好。

class Solution {
    public boolean isValid(String s) {
        Deque<Character> stack = new LinkedList<>();
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') {
                stack.push('(');
            } else if (s.charAt(i) == '{') {
                stack.push('{');
            } else if (s.charAt(i) == '[') {
                stack.push('[');
            } else if (s.charAt(i) == ')' && (stack.size() == 0 || stack.pop() != '(')) {
                return false;
            } else if (s.charAt(i) == '}' && (stack.size() == 0 || stack.pop() != '{')) {
                return false;
            } else if (s.charAt(i) == ']' && (stack.size() == 0 || stack.pop() != '[')) {
                return false;
            }
        }
        return stack.size() == 0;
    }
}

最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

要点在于增加一个栈，和用的栈同步 push 和 pop 数据，只不过 push 的时候 push 进去当前的最小值，pop 的时候同步 pop。

class MinStack {
    Deque<Integer> stack;
    Deque<Integer> minStack;

    public MinStack() {
        stack = new LinkedList<>();
        minStack = new LinkedList<>();
    }
    
    public void push(int val) {
        stack.push(val);
        // 与 stack 同步放入最小值
        if (minStack.size() == 0) {
            minStack.push(val);
        } else {
            minStack.push(Math.min(minStack.peek(), val));
        }
    }
    
    public void pop() {
        stack.pop();
        minStack.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int getMin() {
        return minStack.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

字符串解码

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

1 2	`输入：s = "3[a]2[bc]" 输出："aaabcbc"`

要点：

括号的处理，看到左括号右括号，要想到用栈来解决。
括号前是数字就解析为数字
括号前为字母就加进来
括号中的内容要用解析的数字进行一个重复
记得清空 sb

class Solution {
    public String decodeString(String s) {
        Deque<Integer> numStack = new LinkedList<>();
        Deque<String> strStack = new LinkedList<>();
        int multi = 0;
        StringBuilder sb = new StringBuilder();
        for (char ch : s.toCharArray()) {
            if (ch == '[') {
                numStack.push(multi);
                strStack.push(sb.toString());
                multi = 0;
                sb = new StringBuilder();
            } else if (ch == ']') {
                int times = numStack.pop();
                StringBuilder tmp = new StringBuilder();
                for (int i = 0; i < times; i++) {
                    tmp.append(sb);
                }
                sb = new StringBuilder();
                sb.append(strStack.pop()).append(tmp);
            } else if ('0' <= ch && ch <= '9') {
                multi = multi * 10 + (ch - '0');
            } else {
                sb.append(ch);
            }
        }
        return sb.toString();
    }
}

每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

从右向左

要点：单调栈

栈里面存的是当前 index，当新放进来的温度比栈中已有的温度低的时候，新放进来的温度就有答案了。

否则就更新栈。

image-20250301225057849

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int[] ans = new int[temperatures.length];
        Deque<Integer> tempStack = new LinkedList<>();
        for (int i = temperatures.length - 1; i >= 0; i--) {
            int temp = temperatures[i];
            while (!tempStack.isEmpty() && temp >= temperatures[tempStack.peek()]) {
                tempStack.pop();
            }
            if (!tempStack.isEmpty()) {
                ans[i] = tempStack.peek() - i;
            }
            tempStack.push(i);
        }
        
        return ans;
    }
}

从左向右

单调栈内存放的是 index，然后都是新放进去的 index 大，同时只放进去没有更高温度的 index。

当新给的温度比栈顶的温度高的时候，那些温度就都有救了。

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int n = temperatures.length;
        int[] ans = new int[n];
        Deque<Integer> st = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            int temp = temperatures[i];
            while (!st.isEmpty() && temp > temperatures[st.peek()]) { // 单调栈内比当前小的温度都有救了
                int j = st.pop();
                ans[j] = i - j;
            }
            st.push(i);
        }
        
        return ans;
    }
}

柱状图中最大的矩形

image.png

所以这题的关键在于给定一个柱子，找到左边和右边第一个高度小于给定柱子的下标。

暴力做法就是硬找，给定一个柱子，遍历所有的柱子找到高度更小的。找柱子复杂度为 O（n）。

优化做法就是优化如何得到 left[i] 和 right[i]。

left[i] 表示给定第 i 个柱子，左边第一个比他矮的柱子的下标。

right[i] 表示给定第 i 个柱子，右边第一个比他矮的柱子的下标。

求 left[i] 的方法：从左向右，要求的是比当前柱子高度低的柱子，所以用单调栈使得：单调栈内只留下比当前柱子高度更矮的柱子。然后剩下的这个柱子就是答案。另一种理解方法是：单调栈内比当前柱子高的柱子（更左面更高的柱子）都用不到了

求 right[i] 的方法也是同理：从右向左，要求的是比当前柱子高度低的柱子，所以用单调栈使得：单调栈内只留下比当前柱子高度更矮的柱子。然后剩下的这个柱子就是答案了。另一种理解方法是：单调栈内比当前柱子高的柱子（更右面更高的柱子）都用不到了

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] left = new int[n];
        int[] right = new int[n];
        Deque<Integer> st = new LinkedList<>();
        // 形成 left[i]
        for (int i = 0; i < n; i++) {
            int h = heights[i];
            while (!st.isEmpty() && h <= heights[st.peek()]) { // 左边比当前柱子高的柱子后面用不到了
                st.pop();
            }
            // 栈中剩下的是高度比当前柱子低的柱子的下标
            // 用于后续找更低的柱子
            left[i] = st.isEmpty() ? -1 : st.peek();
            st.push(i);
        }

        // 形成 right[i]
        st.clear();
        for (int i = n - 1; i >= 0; i--) {
            int h = heights[i];
            while (!st.isEmpty() && h <= heights[st.peek()]) { // 右边元素中比当前柱子高的后面也用不到了
                st.pop();
            }
            // 栈中剩下的是高度比当前柱子低的柱子的下标
            // 用于后续找更低的柱子
            right[i] = st.isEmpty() ? n : st.peek();
            st.push(i);
        }

        // 计算最大面积
        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans = Math.max(ans, heights[i] * (right[i] - left[i] - 1));
        }
        return ans;
    }
}

堆

数组中的第 K 个最大元素

快速选择 O(n)

和快排的思路一致：对于一组数据，选择一个基准元素（base），通常选择第一个或最后一个元素，通过第一轮扫描，比base小的元素都在base左边，比base大的元素都在base右边，再有同样的方法递归排序这两部分，直到序列中所有数据均有序为止。

如果有大量相似的元素，那么要二路快排。否则时间复杂度会退化到 O(n^2)。

class Solution {
    public int findKthLargest(int[] nums, int k) {
        int n = nums.length;
        return quickSelect(nums, 0, n - 1, n - k);
    }

    private int quickSelect(int[] nums, int left, int right, int k) {
        if (left == right) return nums[left];
        int pivotIndex = partition(nums, left, right);
        if (k == pivotIndex) {
            return nums[k];
        } else if (k < pivotIndex) {
            return quickSelect(nums, left, pivotIndex - 1, k);
        } else {
            return quickSelect(nums, pivotIndex + 1, right, k);
        }
    }
    
    // 分割点位置
    private int partition(int[] nums, int left, int right) {
        int pivot = nums[right];
        int l = left;
        int r = right - 1;
        while (l <= r) { // 用 l <= r 代替无限循环
            while (l <= r && nums[l] < pivot) l++; // 左指针 l 的行为：当 nums[l] 小于枢轴时，l 会继续向右移动。
            while (l <= r && pivot < nums[r]) r--; // 右指针 r 的行为：当 nums[r] 大于枢纽时，r 会继续向左移动。
            if (l <= r) {
                swap(nums, l, r);
                l++; // 交换后必须移动指针
                r--; // 避免死循环
            }
        }
        swap(nums, l, right); // 将基准放到正确位置，l 指向第一个大于等于 privot 的值
        return l; // 返回基准的最终位置
    }

    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

堆

class Solution {
    public int findKthLargest(int[] nums, int k) {
        int heapSize = nums.length;
        buildMaxHeap(nums, heapSize);
        for (int i = nums.length - 1; i >= nums.length - k + 1; --i) {
            swap(nums, 0, i);
            --heapSize;
            maxHeapify(nums, 0, heapSize);
        }
        return nums[0];
    }

    public void buildMaxHeap(int[] a, int heapSize) {
        for (int i = heapSize / 2 - 1; i >= 0; --i) {
            maxHeapify(a, i, heapSize);
        } 
    }

    public void maxHeapify(int[] a, int i, int heapSize) {
        int l = i * 2 + 1, r = i * 2 + 2, largest = i;
        if (l < heapSize && a[l] > a[largest]) {
            largest = l;
        } 
        if (r < heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            swap(a, i, largest);
            maxHeapify(a, largest, heapSize);
        }
    }

    public void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

前 k 个高频元素

遍历一遍并统计频率，并且放到堆里面。

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        int n = nums.length;
        if (n == k) return nums;
        Arrays.sort(nums);
        PriorityQueue<int[]> queue = new PriorityQueue<>((a, b) -> {
            return b[0] - a[0];
        });
        int count = 1;
        for (int i = 0; i < n; i++) {
            if (i + 1 < n && nums[i] == nums[i + 1]) { // 对边界情况的处理
                count++;
            } else {
                queue.offer(new int[]{count, nums[i]});
                count = 1;
            }
        }
        int[] ans = new int[k];
        for (int i = 0; i < k; i++) {
            ans[i] = queue.poll()[1];
        }
        return ans;
    }
}

数据流的中位数

要点在于：

用两个堆，一个升序保存比中位数大的数，一个降序保存比中位数小的数
这样中位数就是比中位数大的数中最小的和比中位数小的数中最大的两个数的一半

class MedianFinder {
    PriorityQueue<Integer> gtQueue;
    PriorityQueue<Integer> ltQueue;

    public MedianFinder() {
        gtQueue = new PriorityQueue<>((a, b) -> (a - b)); // 升序
        ltQueue = new PriorityQueue<>((a, b) -> (b - a)); // 降序
    }
    
    public void addNum(int num) {
        if (ltQueue.isEmpty() || num <= ltQueue.peek()) {
            ltQueue.offer(num);
            if (ltQueue.size() > gtQueue.size() + 1) {
                gtQueue.offer(ltQueue.poll());
            }
        } else {
            gtQueue.offer(num);
            if (gtQueue.size() > ltQueue.size()) {
                ltQueue.offer(gtQueue.poll());
            }
        }
    }
    
    public double findMedian() {
        if (ltQueue.size() - gtQueue.size() == 1) {
            return ltQueue.peek();
        }
        return (gtQueue.peek() + ltQueue.peek()) / 2.0;
    }
}

技巧

买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

要点：

在每天都卖，买的价格是已出现的最小值。

class Solution {
    public int maxProfit(int[] prices) {
        int ans = 0;
        int n = prices.length;
        int lowest = prices[0];
        for (int i = 1; i < n; i++) {
            int x = prices[i];
            if (x < lowest) {
                lowest = x;
            } else {
                ans = Math.max(ans, x - lowest);
            }
        }
        return ans;
    }
}

跳跃游戏

class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        List<Integer> list = new ArrayList<>();

        // 总体思路：是否存在跳不过去的 0
        for (int i = 0; i < n; i++) {
            if (nums[i] == 0 && i != n - 1) { // 最后的一个 0 不用判断
                list.add(i);
            }
        }

        int lastStart = 0;
        for (int i = 0; i < list.size(); i++) {
            // 看 0 的前面
            boolean ok = false;
            for (int j = list.get(i) - 1; j >= lastStart; j--) {
                if (nums[j] > list.get(i) - j) {
                    ok = true;
                }
            }
            if (!ok) {
                return false;
            }
        }
        return true;
    }
}

官解：判断能跳过去的最大长度是否超过结尾

public class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        int rightmost = 0;
        for (int i = 0; i < n; ++i) {
            if (i <= rightmost) {
                rightmost = Math.max(rightmost, i + nums[i]);
                if (rightmost >= n - 1) {
                    return true;
                }
            }
        }
        return false;
    }
}

x 的平方根

二分

class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}

转换为对数

对于平方根有以下运算：

$\sqrt{x} = x^{1/2} = \left(e^{\ln x}\right)^{1/2} = e^{\frac{1}{2} \ln x}$

class Solution {
    public int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        int ans = (int) Math.exp(0.5 * Math.log(x));
        return (long) (ans + 1) * (ans + 1) <= x ? ans + 1 : ans;
    }
}

子串

和为 K 的子数组

2 * 10^4 O(n^2) 或者 O(n)

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。

子数组是数组中元素的连续非空序列。

前缀和

class Solution {
    public int subarraySum(int[] nums, int k) {
        int left = 0, n = nums.length, right = n - 1, ans = 0;;
        int[] sum = new int[n];
        sum[0] = nums[0];
        for (int i = 1; i < n; i++) {
            sum[i] = sum[i - 1] + nums[i];
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (sum[j] - sum[i] == k) { // 这种写法无法计算前 n 个的和
                    ans++;
                }
            }
            
        }
        for (int i = 0; i < n; i++) { // 补上
            if (sum[i] == k) {
                ans++;
            }
        }
        return ans;
    }
}

优化前缀和中的 O(n^2)

用 “两数之和” 的思路来优化掉枚举所有前缀和的过程，用 HashMap 直接找到想要的前缀和。

class Solution {
    public int subarraySum(int[] nums, int k) {
        int left = 0, n = nums.length, right = n - 1, ans = 0;;
        int[] sum = new int[n];
        sum[0] = nums[0];
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 1; i < n; i++) {
            sum[i] = sum[i - 1] + nums[i];
        }
        // 方法一：暴力前缀和 

        // for (int i = 0; i < n; i++) {
        //     for (int j = i + 1; j < n; j++) {
        //         if (sum[j] - sum[i] == k) { // 这种写法无法计算前 n 个的和
        //             ans++;
        //         }
        //     }
        // }

        // 方法一的实质是求两数之差为固定值的数有多少
        // sum[j] - sum[i] = k
        // 用 "两数之和" 的方法用哈希表进行优化 a + b = target -> a = target - b
        for (int i = 0; i < n; i++) {
            int num = k + sum[i];
            if (map.containsKey(sum[i])) { // 如果需要的正好有
                ans += map.get(sum[i]);
            }
            map.put(num, map.getOrDefault(num, 0) + 1); // 需要 k + sum[i]
        }

        for (int i = 0; i < n; i++) { // 补上
            if (sum[i] == k) {
                ans++;
            }
        }
        return ans;
    }
}

滑动窗口最大值

10^5 O(n) 可以做

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

像前缀和一样，维护区间的最大值呢？

ST 表

复杂度为 O(nlogn)：

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length, l = 0, logN = (int)(Math.log(n) / Math.log(2)) + 1;
        int[] result = new int[n - k + 1];
        int f[][] = new int[n + 1][logN];
        int[] logn = new int[n + 5];

        for (int i = 1; i <= n; i++) {
            f[i][0] = nums[i - 1];
        }

        // pre
        logn[1] = 0;
        logn[2] = 1;
        for (int i = 3; i < n; i++) {
            logn[i] = logn[i / 2] + 1;
        }

        for (int j = 1; j <= logN; j++)
            for (int i = 1; i + (1 << j) - 1 <= n; i++)
                f[i][j] = Math.max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);  // ST表具体实现
        for (int i = 1; i <= n - k + 1; i++) {
            int x = i, y = Math.min(n, i + k - 1);
            int s = logn[y - x + 1];
            result[i-1] = Math.max(f[x][s], f[y - (1 << s) + 1][s]);
        }
        return result;
    }
}

优先队列

O(nlogn)

这里的思路是用一个堆来维护最大值，同时在堆中记录下最大值的下标，当左指针移动时，要删掉那些失效的最大值。

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        PriorityQueue<Map.Entry<Integer, Integer>> pq = new PriorityQueue<>((a, b) -> b.getKey() - a.getKey());
        int n = nums.length, l = 0;
        int ret[] = new int[n - k + 1];
        for (int r = 0; r < n; r++) {
            pq.offer(new java.util.AbstractMap.SimpleEntry<>(nums[r], r));
            if (r - l + 1 == k) {
                while (pq.peek().getValue() < l) pq.poll();
                ret[r - k + 1] = pq.peek().getKey();
                l++;
            }
        }
        return ret;
    }
}

单调队列

O(n)

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length, l = 0;
        int[] ans = new int[n - k + 1];
        Deque<Integer> deque = new LinkedList<Integer>(); // 递增存储下标
        for (int r = 0; r < n; r++) {
            while (!deque.isEmpty() && nums[r] > nums[deque.peekLast()]) { // 放进去的是保持下标递增的情况下值最大的
                deque.pollLast();
            }
            deque.offerLast(r);
            if (r - l + 1 == k) {
                ans[l] = nums[deque.peekFirst()];
                while (!deque.isEmpty() && deque.peekFirst() <= l) { // 淘汰掉滑动窗口以外的
                    deque.pollFirst();
                }
                l++;
            }
        }
        return ans;
    }
}

分块 + 前后缀数组

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        if (n == 1) return nums;
        int[] prefixMax = new int[n]; // 以 i 结尾的前缀最大值，也就是查询的左边
        int[] suffixMax = new int[n]; // 以 i 开头的后缀最大值，也就是查询的右边
        // [ a, b, c ] [ d, e, f ]
        // 按 k 分块，如果是边界，那么需要第一个的后缀最大值和第二个的前缀最大值拼起来
        // 如果不是边界，那么直接取后缀最大值就好
        for (int i = 0; i < n; i++) {
            if (i % k == 0) { // 边界
                prefixMax[i] = nums[i];

            } else { // 在块中间
                prefixMax[i] = Math.max(prefixMax[i - 1], nums[i]);
            }
        }
        for (int i = n - 1; i >= 0; i--) {
            if ((i + 1) % k == 0 || i == n - 1) {
                suffixMax[i] = nums[i];
            } else {
                suffixMax[i] = Math.max(suffixMax[i + 1], nums[i]);
            }
        }

        int[] ans = new int[n - k + 1];
        // [ a, b, c ] [ d, e, f ]
        for (int i = 0 ; i < n - k + 1; i++) { // 滑动窗口开始位置
            if (i % k == 0) { // 边界
                ans[i] = prefixMax[i + k - 1];
            } else { // [ a, b, c ] [ d, e, f ]
                     // b 为滑动窗口开始的时候，元素为 b, c, d，最大值为 max([b, c], [d])
                     // -> max(suffixMax[1], prefixMax[3])
                ans[i] = Math.max(suffixMax[i], prefixMax[i + k - 1]);
            }
        }
        return ans;


    }
}

最小覆盖子串

要点：

滑动窗口走过所有的子串
用哈希表判断是否涵盖所有字符

class Solution {
    Map<Character, Integer> tMap = new HashMap<>();
    Map<Character, Integer> windowMap = new HashMap<>();

    public String minWindow(String s, String t) {
        // 滑动窗口，用哈希表判断是否涵盖所有字符
        int n = s.length();
        int l = 0;
        int ansL = 0, ansR = -1, ansLen = Integer.MAX_VALUE;

        for (char ch : t.toCharArray()) {
            tMap.put(ch, tMap.getOrDefault(ch, 0) + 1);
        }

        for (int r = 0; r < n; r++) {
            windowMap.put(s.charAt(r), windowMap.getOrDefault(s.charAt(r), 0) + 1);
            while (l <= r && check()) {
                if (r - l + 1 < ansLen) {
                    ansL = l;
                    ansR = r;
                    ansLen = r - l + 1;
                }
                windowMap.put(s.charAt(l), windowMap.getOrDefault(s.charAt(l), 1) - 1);
                l++;
            }
        }
        return ansR == -1 ? "" : s.substring(ansL, ansR + 1);
    }

    private boolean check() {
        for (Map.Entry<Character, Integer> entry : tMap.entrySet()) {
            if (windowMap.getOrDefault(entry.getKey(), 0) < entry.getValue()) {
                return false;
            }
        }
        return true;
    }
}

双指针

前后指针：经典的一个 pre 指针，一个 cur 指针：可以解决反转链表、交换节点等问题。
快慢指针：还有一个 fast 指针，一个 slow 指针：可以解决删除第 n 个元素的问题。

19.删除链表的倒数第 N 个结点

两个间隔 n 个节点的指针，快指针到末尾的时候，慢指针就是倒数第 n 个节点。

142.环形链表 II

判断链表是否有环，如果有返回入环的第一个节点

根据题意，任意时刻，fast 指针走过的距离都为 slow 指针的 2 倍。因此，我们有

a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)
有了 a=c+(n−1)(b+c) 的等量关系，我们会发现：从相遇点到入环点的距离加上 n−1 圈的环长，恰好等于从链表头部到入环点的距离。

因此，当发现 slow 与 fast 相遇时，我们再额外使用一个指针 ptr。起始，它指向链表头部；随后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇。

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while (slow != null && fast != null && slow.next != null && fast.next != null && fast.next.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) { // 有环
                ListNode index1 = fast;
                ListNode index2 = head;
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
    }
}

哈希表

两数之和

10^4 O(n)

一个哈希表

三数之和

3000

O(n^2)

排序+双指针

四数之和

排序+双指针

注意溢出

四数相加

与上一题不同在于有 4 个数组，4 个数组等长度，上一题每个区间长度不同

哈希表 + 哈希表

字母异位词分组

10^4 O(n) 或 O(nlogn)

主要考虑异位词表示为相同的 map key，这样就可以将异位词聚集在一起。

最长连续序列

10^5 O(n)

未排序的数组，O(n) 找到数字连续的最长序列，不要求在原数组中连续。

排序做法为 O(nlogn)

key：考虑某一个数是不是连续序列的第一个数字，如果是则继续往下。

for (int num : set) {
    int i = 1;
    while (set.contains(num + i)) {
        i++;
        longest = Math.max(longest, i);
    }
}

这种写法最坏会变成 O(n^2)，需要思考如何跳过重复情况。如果再开一个 TreeSet 来定位下一个数字是 O(logn)，应该可以。

class Solution {
    public int longestConsecutive(int[] nums) {
        if (nums.length == 0) return 0;
        Set<Integer> set = new HashSet<>();
        TreeSet<Integer> treeSet = new TreeSet<>();
        Integer next = 0x3f3f3f3f;
        for (int i = 0; i < nums.length; i++) {
            set.add(nums[i]);
            treeSet.add(nums[i]);
            next = Math.min(next, nums[i]);
        }
        int longest = 1;
        while (next != null) {
            int i = 1;
            while (set.contains(next)) {
                next = next + 1;
                longest = Math.max(longest, i);
                i++;
            }
            next = treeSet.higher(next); // 定位下一个数字
        }

        return longest;
    }
}

还有一种 O(1) 定位下一个数字的方法：

如果这个数字为 x，那么不存在 x-1 的话，这个数字一定是连续序列的第一个数字。

class Solution {
    public int longestConsecutive(int[] nums) {
        if (nums.length == 0) return 0;
        Set<Integer> set = new HashSet<>();
        for (int i = 0; i < nums.length; i++) {
            set.add(nums[i]);
        }
        int longest = 1;
        for (int num : set) {
            if (set.contains(num - 1)) continue;
            int i = 1;
            while (set.contains(num + i)) {
                i++;
                longest = Math.max(longest, i);
            }
        }

        return longest;
    }
}

使数组的值全部为 K 的最少操作次数

给你一个整数数组 nums 和一个整数 k 。

如果一个数组中所有 严格大于 h 的整数值都相等，那么我们称整数 h 是 合法的 。

比方说，如果 nums = [10, 8, 10, 8] ，那么 h = 9 是一个合法整数，因为所有满足 nums[i] > 9 的数都等于 10 ，但是 5 不是合法整数。

你可以对 nums 执行以下操作：

选择一个整数 h ，它对于当前 nums 中的值是合法的。

对于每个下标 i ，如果它满足 nums[i] > h ，那么将 nums[i] 变为 h 。

你的目标是将 nums 中的所有元素都变为 k ，请你返回最少操作次数。如果无法将所有元素都变 k ，那么返回 -1 。

其实就是把大的数字变小，需要变几次。

我的做法：用 SortedSet 统计大于 k 的有多少，以及是否有小于 k 的。

class Solution {
    // 也就是说可以把大的变小
    public int minOperations(int[] nums, int k) {
        SortedSet<Integer> set = new TreeSet<>();
        for (int num : nums) {
            set.add(num);
        }
        if (set.first() < k) return -1;
        if (set.first() == k) return set.size() - 1;
        return set.size();
    }
}

官解：

class Solution {
    public int minOperations(int[] nums, int k) {
        Set<Integer> st = new HashSet<>();
        for (int x : nums) {
            if (x < k) {
                return -1;
            } else if (x > k) {
                st.add(x);
            }
        }
        return st.size();
    }
}

统计坏数对的数目

给你一个下标从 0 开始的整数数组 nums 。如果 i < j 且 j - i != nums[j] - nums[i] ，那么我们称 (i, j) 是一个 坏数对 。

请你返回 nums 中 坏数对 的总数目。

正难则反，考虑坏数对的个数=总数对-好数对。

好数对：j - i == nums[j] - nums[i] 得到 j - nums[j] = nums[i] - i

于是有：

class Solution {
    public long countBadPairs(int[] nums) {
        int n = nums.length;
        long ans = (long)n * (n - 1) / 2;
        Map<Long, Long> map = new HashMap<>();
        for (int i = 0; i < n; i++) {
            long x = nums[i] - i;
            long c = map.getOrDefault(x, 0L);
            ans -= c;
            map.put(x, c + 1);
        }
        return ans;
    }
}

字符串

KMP 算法

next 数组：是一个前缀表，前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

那么什么是前缀表：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀和后缀字符串是子字符串aa ，因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面重新匹配就可以了。

反转字符串中的单词

方法一：split 之后拼接。

1	`"a good example".split() // [a, good, , , example]，分割后存在 ""`

方法二：反转整个字符串之后，再反转单个字符串。

最长公共子串

状态转移方程如下，dp[i][j] 表示字符串 x 以 i 结尾，字符串 y 以 j 结尾的最长公共子串，这样就有了：

$d p[i][j]=\left\{\begin{array}{l} d p[i-1][j-1]+1, \text { 当且仅当 } x[i]=y[j] \\ 0, \text { 当 } x[i] \ne y[j] \end{array}\right.$

按照上面方程实现的算法时间复杂度为 $O(n^2)$，空间复杂度为 $O(n^2)$。

image.png

注意到，更新 $dp[i][j]$ 只需要上一列，即 $dp[i-1]$ 列，所以可以将空间复杂度降低为 $O(n)$，但是需要注意因为使用的是相同的数组列，所以字符串不相等时需要设置 $dp[j] = 0$，同时要注意从后向前更新数组，因为如果从前向后更新，那么当前的 $dp[j]$ 使用的是当前列刚刚更新过的数据，而我们需要的是上一列的数据，所以可以从后向前更新数据避免这个问题。

rust 代码如下：

let mut dp = vec![0; s2.len()];
for i in 0..s1.len() {
    // 逆序迭代是因为更新a[i][j]需要a[i-1][j-1]
    // 现在是一个数组，所以 a[j] 是原来的 a[i][j]，而我们需要的是 a[i-1][j]
    // 所以从后向前迭代，a[j] 是原来的 a[i-1][j]
    for j in (0..s2.len()).s2() {
        if s[i] == s2[j] {
            if i == 0 || j == 0 {
                dp[j] = 1;
            } else {
                dp[j] = dp[j - 1] + 1;
            }
            if dp[j] > max_len {
                let before_s2 = s2.len() - 1 - j;
                if before_s2 + dp[j] - 1 == i {
                    max_len = dp[j];
                    max_end = i;
                }
            }
        } else {
            // 与之前不同，之前使用的是不同的列，所以不需要置0
            dp[j] = 0;
        }
    }
}

最长回文子串

动态规划

将字符串倒置之后求最长公共子串（状态转移方程与最长公共子串相同），并判断是否为回文子串，这里回文子串「由倒置字符串推出的原字符串末尾下标」与「i」应该相等。

代码中 longest_palindrome1 的求最长公共子串空间复杂度为 $O(n^2)$，longest_palindrome2 的求最长公共子串空间复杂度为 $O(n)$。

代码如下：

struct Solution;

impl Solution {
    pub fn longest_palindrome1(s: String) -> String {
        if s.len() <= 1 {
            return s;
        }
        let rev: String = s.chars().rev().collect();
        let rev = rev.as_bytes();
        let s = s.as_bytes();
        let mut dp = vec![vec![0; rev.len()]; s.len()];
        let mut max_len = 0;
        let mut max_end = 0;
        for i in 0..s.len() {
            for j in 0..rev.len() {
                if s[i] == rev[j] {
                    if i == 0 || j == 0 {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = dp[i - 1][j - 1] + 1;
                    }
                }
                if dp[i][j] > max_len {
                    // 如果是回文串，那么「由倒置字符串推出的原字符串末尾下标」与「i」应该相等
                    // 其中，倒置字符串的 rev.len() - 1 - j，也就是倒置之前的开始下标，减一是因为长度比下标多一
                    // 再加上 dp[i][j] - 1，就是原字符串的末尾下标。abc，a的下标为0，长度为3，0+3为3，但是最大下标为2，所以需要减一
                    let before_rev = rev.len() - 1 - j;
                    if before_rev + dp[i][j] - 1 == i {
                        max_len = dp[i][j];
                        max_end = i;
                    }
                }
            }
        }
        std::str::from_utf8(&s[max_end + 1 - max_len..max_end + 1])
            .unwrap()
            .to_string()
    }
    pub fn longest_palindrome2(s: String) -> String {
        if s.len() < 1 {
            return s;
        }
        let rev: String = s.chars().rev().collect();
        let s = s.as_bytes();
        let rev = rev.as_bytes();
        let mut max_len = 0;
        let mut max_end = 0;
        let mut dp = vec![0; rev.len()];
        for i in 0..s.len() {
            // 逆序迭代是因为更新a[i][j]需要a[i-1][j-1]
            // 现在是一个数组，所以 a[j] 是原来的 a[i][j]，而我们需要的是 a[i-1][j]
            // 所以从后向前迭代，a[j] 是原来的 a[i-1][j]
            for j in (0..rev.len()).rev() {
                if s[i] == rev[j] {
                    if i == 0 || j == 0 {
                        dp[j] = 1;
                    } else {
                        dp[j] = dp[j - 1] + 1;
                    }
                    if dp[j] > max_len {
                        let before_rev = rev.len() - 1 - j;
                        if before_rev + dp[j] - 1 == i {
                            max_len = dp[j];
                            max_end = i;
                        }
                    }
                } else {
                    // 与之前不同，之前使用的是不同的列，所以不需要置0
                    dp[j] = 0;
                }
            }
        }
        std::str::from_utf8(&s[max_end + 1 - max_len..max_end + 1])
            .unwrap()
            .to_string()
    }
}

中心拓展算法

为了避免在之后的叙述中出现歧义，这里我们指出什么是“朴素算法”。

该算法通过下述方式工作：对每个中心位置 $i$ 在比较一对对应字符后，只要可能，该算法便尝试将答案加 $1$。

该算法是比较慢的：它只能在 $O(n^2)$ 的时间内计算答案。

该算法的实现如下：

// C++ Version
vector<int> d1(n), d2(n);
for (int i = 0; i < n; i++) {
  d1[i] = 1;
  while (0 <= i - d1[i] && i + d1[i] < n && s[i - d1[i]] == s[i + d1[i]]) {
    d1[i]++;
  }

  d2[i] = 0;
  while (0 <= i - d2[i] - 1 && i + d2[i] < n &&
         s[i - d2[i] - 1] == s[i + d2[i]]) {
    d2[i]++;
  }
}

# Python Version
d1 = [0] * n
d2 = [0] * n
for i in range(0, n):
    d1[i] = 1
    while 0 <= i - d1[i] and i + d1[i] < n and s[i - d1[i]] == s[i + d1[i]]:
        d1[i] += 1

    d2[i] = 0
    while 0 <= i - d2[i] - 1 and i + d2[i] < n and s[i - d2[i] - 1] == s[i + d2[i]]:
        d2[i] += 1

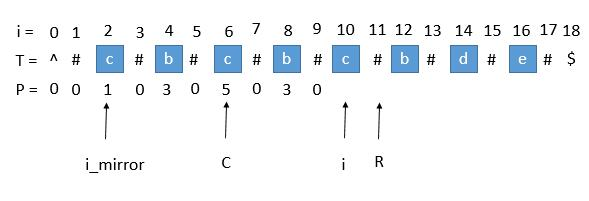
Manacher 算法¹²

Manacher 算法是对中心拓展算法的优化，为了快速计算，我们维护已找到的最靠右的子回文串的 边界 $(l, r)$（即具有最大 $r$ 值的回文串，其中 $l$ 和 $r$ 分别为该回文串左右边界的位置）。初始时，我们置 $l = 0$ 和 $r = -1$（-1需区别于倒序索引位置，这里可为任意负数，仅为了循环初始时方便）。

现在假设我们要对下一个 $i$ 计算 $P[i]$，而之前所有 $P[]$ 中的值已计算完毕。我们将通过下列方式计算：

如果 $i$ 位于当前子回文串之外，即 $i > r$，那么我们调用朴素算法。

因此我们将连续地增加 $d_1[i]$，同时在每一步中检查当前的子串 $[i - P[i] \dots i + P[i]]$（$P[i]$ 表示半径长度，下同）是否为一个回文串。如果我们找到了第一处对应字符不同，又或者碰到了 $s$ 的边界，则算法停止。在两种情况下我们均已计算完 $P[i]$。此后，仍需记得更新 $(l, r)$。
现在考虑 $i \le r$ 的情况。我们将尝试从已计算过的 $P[]$ 的值中获取一些信息。首先在子回文串 $(l, r)$ 中反转位置 $i$，即我们得到 $j = l + (r - i)$。现在来考察值 $P[j]$。因为位置 $j$ 同位置 $i$ 对称，我们 几乎总是 可以置 $P[i] = P[j]$。

存在 棘手的情况，主要有以下：
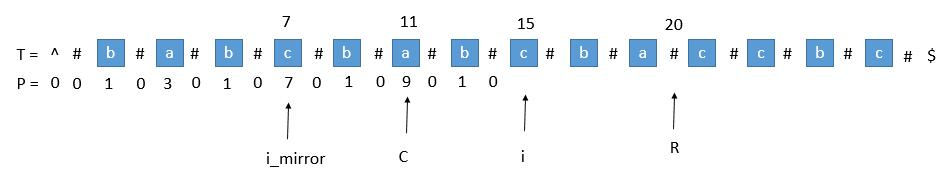
- 超出了 $r$
  
  图转自 LeetCode
  
  当我们要求 $P [ i ]$ 的时候，$P [mirror] = 7$，而此时 $P [ i ]$ 并不等于 $7$，为什么呢，因为我们从 $i$ 开始往后数 $7$ 个，等于 $22$，已经超过了最右的 $r$，此时不能利用对称性了，但我们一定可以扩展到 $r$ 的，所以 $P [ i ]$ 至少等于 $r - i = 20 - 15 = 5$，会不会更大呢，我们只需要比较 $T [ r+1 ]$ 和 $T [ r+1 ]$ 关于 $i$ 的对称点就行了，就像中心扩展法一样一个个扩展。
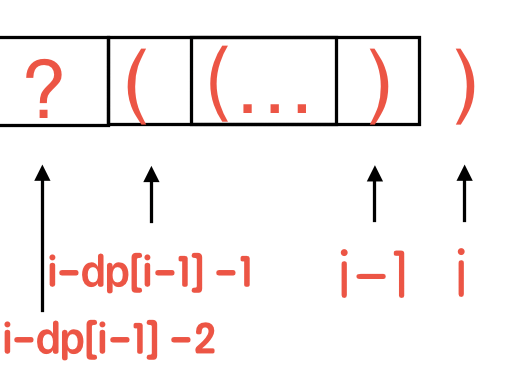
- $P[i]$ 遇到了原字符串的左边界
  
  image.png
  
  此时$P [ i_{mirror} ] = 1$，但是 $P [ i ]$ 赋值成 1 是不正确的，出现这种情况的原因是 $P [ i_{mirror} ]$ 在扩展的时候首先是 “#” == “#”，之后遇到了 “^” 和另一个字符比较，也就是到了边界，才终止循环的。而 $P [ i ]$ 并没有遇到边界，所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。
- $i = r$
  
  此时我们先把 P [ i ] 赋值为 0，然后通过中心扩展法一步一步扩展就行了。
考虑 $r$ 的更新

就这样一步一步的求出每个 $P [ i ]$，当求出的 $P [ i ]$ 的右边界大于当前的 $r$ 时，我们就需要更新 $r$ 为当前的回文串了。

最长公共子序列（LCS）

动态规划

状态转移方程如下：

$d p[i][j]=\left\{\begin{array}{ll} d p[i-1][j-1]+1, & t e x t_{1}[i-1]=t e x t_{2}[j-1] \\ \max (d p[i-1][j], d p[i][j-1]), & t e x t_{1}[i-1] \neq t e x t_{2}[j-1] \end{array}\right.$

LCS 对应的状态转移方程与最长公共子串不同之处在于：

最长公共子串要求字符串连续，所以下一个状态只能由上一个对应的字符串得到。
LCS 不要求字符串连续，所以可以前后移动，就有了第二个式子。

知道状态定义之后，我们开始写状态转移方程。

当 $text_1[i - 1] = text_2[j - 1]$ 时，说明两个子字符串的最后一位相等，所以最长公共子序列又增加了 1，所以 $dp[i][j] = dp[i - 1][j - 1] + 1$；举个例子，比如对于 ac 和 bc 而言，他们的最长公共子序列的长度等于 a 和 b 的最长公共子序列长度 $0 + 1 = 1$。
当 $text_1[i - 1] \ne text_2[j - 1]$ 时，说明两个子字符串的最后一位不相等，那么此时的状态 $dp[i][j]$ 应该是 $dp[i - 1][j]$ 和 $dp[i][j - 1]$ 的最大值。举个例子，比如对于 ace 和 bc 而言，他们的最长公共子序列的长度等于

① ace 和 b 的最长公共子序列长度 0 与

② ac 和 bc 的最长公共子序列长度 1 的最大值，即 1。

代码如下：

struct Solution;

impl Solution {
    pub fn longest_common_subsequence(text1: String, text2: String) -> i32 {
        let text1 = text1.as_bytes();
        let text2 = text2.as_bytes();
        let m = text1.len();
        let n = text2.len();
        // dp[i][j] 代表 text1[0..i] 与 text2[0..j] 的最大子序列，注意不包括第 i 和第 j 个字符
        // 同理，dp 数组要循环到 m 与 n 才结束
        let mut dp = vec![vec![0; n + 1]; m + 1];
        for i in 1..=m {
            for j in 1..=n {
                // 这里要注意，比较的是第 i-1 与第 j-1 个字符
                if text1[i - 1] == text2[j - 1] {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = std::cmp::max(dp[i][j - 1], dp[i - 1][j]);
                }
            }
        }
        return dp[m][n];
    }
}

动态规划

动态规划总结

基本步骤：

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

对于动态规划，可以先初始化一个 dp 数组，然后手写出 dp[0] dp[1] dp[2] dp[3] 等等。这一步可以帮助思考 dp 数组和确定递推公式。

使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

要点：

dp[i] 为到达第 n 层的最低花费
可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯，dp[0] = 0，dp[1] = 0
第 i 层可以从 i - 1 和 i - 2 过来，从 i - 1 过来的花费是 cost[i - 1]，从 cost[i - 2] 过来的花费是 cost[i - 2]

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int[] dp = new int[n + 1]; // 到达第 n 层的最低花费
        dp[0] = 0;
        dp[1] = 0;
        for (int i = 2; i <= n; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[n];
    }
}

杨辉三角

主要难点在处理边界情况

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> ret = new ArrayList<>();
        for (int i = 1; i <= numRows; i++) {
            List<Integer> arr = new ArrayList<>(i);
            for (int j = 0; j < i; j++) {
                arr.add(0);
            }
            arr.set(0, 1);
            arr.set(i - 1, 1);
            List<Integer> lastArr;
            if (ret.size() >= 2) {
                lastArr = ret.get(ret.size() - 1);
                for (int j = 1; j < i - 1; j++) { // 跳过第一个和最后一个
                    arr.set(j, lastArr.get(j-1) + lastArr.get(j));
                }
            }
            ret.add(arr);
        }
        return ret;
    }
}

打家劫舍

要点在于对于某一个房子是否抢劫以及边界处理。

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if (n == 1) return nums[0];
        if (n == 2) return Math.max(nums[0], nums[1]);
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = nums[0];
        dp[2] = Math.max(nums[0], nums[1]);
        for (int i = 3; i <= n; i++) {
            dp[i] = Math.max(dp[i - 2] + nums[i - 1], dp[i - 1]);
        }
        return dp[n];
    }
}

最大子序和

要点在于当前数字结尾的最大子串的和只能来自于前一个，也就是上楼梯只能由前一个上过来，或者现在新开一个。

class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n + 1]; // 第 i 个数结尾的子数组最大值
        int ans = -0x3f3f3f3f;
        for (int i = 1; i <= n; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i - 1], nums[i - 1]);
            ans = Math.max(ans, dp[i]);
        }
        return ans;
    }
}

完全平方数

动态规划

要点是 dp[i] 表示结果为 i 的最少数量，然后转移的话，dp[i] 只能从 dp[i - 所有平方数] 来，于是写出状态转移方程。

class Solution {
    public int numSquares(int n) {
        if (n == 1) return 1;
        if (n == 2) return 2;
        if (n == 3) return 3;
        if (n == 4) return 1;
        if (n == 5) return 2;
        int sqrtN = (int)Math.sqrt(n) + 1;
        int[] square = new int[sqrtN];
        for (int i = 1; i < sqrtN; i++) {
            square[i] = i * i;
        }
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 3;
        dp[4] = 1;
        dp[5] = 2;

        for (int i = 1; i <= n; i++) {
            int min = 999;
            for (int j = 1; j < sqrtN; j++) {
                if (i - square[j] >= 0) {
                    min = Math.min(dp[i - square[j]] + 1, min);
                }
            }
            dp[i] = min;
        }

        return dp[n];
    }
}

优化一下

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            int min = 999;
            for (int j = 1; j * j <= i; j++) {
                if (i - j * j >= 0) {
                    min = Math.min(dp[i - j * j] + 1, min);
                }
            }
            dp[i] = min;
        }

        return dp[n];
    }
}

四平方和定理

image-20250107155619501

零钱兑换

这是一个完全背包问题，硬币可以重复使用。与爬楼梯类似。

$dp[i] = dp[i - coins[j]] + 1$。

class Solution {
    public int coinChange(int[] coins, int amount) {
        if (amount == 0) return 0;
        int n = coins.length;
        int[] dp = new int[Math.max(n, amount) + 10]; // 可以凑成 n 所需的最少的硬币个数
        // 与爬楼梯一样，dp[i] 可以从 dp[i - coins[j]] 过来
        for (int i = 0; i < n; i++) {
            if (coins[i] > amount) {
                continue;
            }
            dp[coins[i]] = 1;
        }
        for (int i = 0; i <= amount; i++) {
            if (dp[i] == 0) {
                dp[i] = 0x3f3f3f3f;
            }
        }
        dp[0] = 0;
        int max = 0;
        for (int i = 1; i <= amount; i++) {
            for (int j = 0; j < n; j++) {
                if (i - coins[j] >= 0) {
                    dp[i] = Math.min(dp[i - coins[j]] + 1, dp[i]);
                }
            }
        }

        return dp[amount] == 0x3f3f3f3f ? -1 : dp[amount];
    }
}

单词拆分

1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20

模拟 + 剪枝

不断地尝试所有可能的拼接，看最后能否拼接出来，注意要剪枝，否则会超时。

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int n = wordDict.size();
        Set<String> dp = new HashSet<>();
        int maxLen = 0x3f3f3f3f;
        for (int i = 0; i < n; i++) {
            String word = wordDict.get(i);
            if (s.startsWith(word)) // 剪枝
                dp.add(word);
            maxLen = Math.min(maxLen, word.length());
        }


        while (maxLen < s.length()) {
            Set<String> tmp = new HashSet<>(dp); // 创建一个临时副本用于遍历
            int minLen = 0x3f3f3f3f;
            for (String cur : tmp) {
                if (cur.length() < maxLen) continue;
                for (int i = 0; i < n; i++) {
                    String newString = cur + wordDict.get(i);
                    if (s.startsWith(newString)) { // 剪枝
                        minLen = Math.min(newString.length(), minLen);
                        dp.add(newString);
                    }
                }
            }
            maxLen = Math.max(maxLen, minLen);
        }
        return dp.contains(s);
    }
}

优化一下

动态规划

image-20250107182951481

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int n = wordDict.size();
        Set<String> set = new HashSet<>(wordDict);
        boolean[] dp = new boolean[s.length() + 1];
        dp[0] = true;
        for (int i = 1; i <= s.length(); i++) {
            for (int j = 0; j < i; j++) {
                if (dp[j] && set.contains(s.substring(j, i))) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[s.length()];
    }
}

最长递增子序列

要点在于 dp 为以第 i 个数字结尾的最长上升子序列长度，也就是 dp[i] 是 i 被选择的情况下的最长上升子序列长度。

这题要求的是子序列，而不是子数组，也就是可以跳过一些数字，所以动态转移方程就是对于 dp[i] 可以从任意的 dp[i - j] 跳过来。

class Solution {
    public int lengthOfLIS(int[] nums) {
        int n =  nums.length, max = 1;
        int[] dp = new int[n + 1]; // 以第 i 个数字结尾的最长上升子序列长度
        for (int i = 1; i <= n; i++) {
            dp[i] = 1; // 如果选当前的 i，至少有 1 个长度
            for (int j = 1; j < i; j++) {
                if (nums[i - 1] > nums[j - 1]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            max = Math.max(max, dp[i]);
        }
        return max;
    }
}

乘积最大子数组

dp_max[i] 表示以第 i 个元素结尾的连续子数组的最大乘积。

对于每一个 dp[i] 来说，他会从前一个最大的 dp[i - 1] 过来，或者从最小的 dp[i - 1] 过来，或者在当前位置另起炉灶。与子序列不同，dp[i] 的子数组只能从 dp[i - 1] 过来，而不能从任意的 dp[i - j] 过来。

class Solution {
    public int maxProduct(int[] nums) {
        if (nums.length == 0) return 0;
        int n = nums.length;
        int[] dp_max = new int[n];
        int[] dp_min = new int[n];
        dp_max[0] = nums[0];
        dp_min[0] = nums[0];
        int ans = nums[0];
        for (int i = 1; i < n; i++) {
            dp_max[i] = Math.max(Math.max(dp_max[i-1] * nums[i], dp_min[i-1] * nums[i]), nums[i]);
            dp_min[i] = Math.min(Math.min(dp_max[i-1] * nums[i], dp_min[i-1] * nums[i]), nums[i]);
            ans = Math.max(ans, dp_max[i]);
        }
        return ans;
    }
}

分割等和子集

1 <= nums.length <= 200，1 <= nums[i] <= 100 数据范围暗示了是和数组中最大数有关的二维 dp

给你一个 只包含正整数 的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

如何将该问题转换为具有最优子结构的问题是难点。

动态规划，时间复杂度与元素大小相关的。

这个问题可以转换为：给定一个只包含正整数的非空数组 nums[0]，判断是否可以从数组中选出一些数字，使得这些数字的和等于整个数组的元素和的一半。因此这个问题可以转换成「0−1 背包问题」。这道题与传统的「0−1 背包问题」的区别在于，传统的「0−1 背包问题」要求选取的物品的重量之和不能超过背包的总容量，这道题则要求选取的数字的和恰好等于整个数组的元素和的一半。类似于传统的「0−1 背包问题」，可以使用动态规划求解。

关键在于：将这个数组分割成两个子集 = 选出的数字的和是数组一半

然后关键的转移方程为：

和为 j 的数字可以由 j - nums[i]（如果存在的话）得到
和为 j 的数字可以由 j （如果存在的话）得到

class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length, target = 0, max = 0;
        for (int i = 0; i < n; i++) {
            target += nums[i];
            max = Math.max(max, nums[i]);
        }
        if ((target & 1) == 1) return false; // 奇数
        else target /= 2;
        if (max > target) return false;

        boolean[][] dp = new boolean[n][target + 1]; // 0..i 的数字中是否存在方案使得和为 j
        // 数字 nums[i] 所在的行都能使得和为 nums[i]
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                dp[i][nums[j]] = true;
            }
        }

        // 0..i 中怎么选都能使得和为 0
        for (int i = 0; i < n; i++) {
            dp[i][0] = true;
        }

        // 和为 j 的数字可以由 j - nums[i]（如果存在的话） 得到
        // 和为 j 的数字可以由 j （如果存在的话）得到
        // 可以根据上面的内容对 dp 数组进行填表
        for (int i = 1; i < n; i++) {
            for (int j = 1; j <= target; j++) {

                if (j >= nums[i]) {

                    dp[i][j] = dp[i - 1][j] | dp[i - 1][j - nums[i]];

                    // 与上面的内容等价
                    // if (dp[i - 1][j - nums[i]]) {
                    //     dp[i][j] = true;
                    // }
                    // if (dp[i - 1][j]) {
                    //     dp[i][j] = true;
                    // }

                } else {
                    dp[i][j] = dp[i - 1][j];

                    // 与上面的内容等价
                    if (dp[i - 1][j]) {
                        dp[i][j] = true;
                    }
                }
            }
        }

        
        return dp[n - 1][target];
    }
}

然后又有这一行仅仅由上一行确定得到，于是有：

class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length, target = 0, max = 0;
        for (int i = 0; i < n; i++) {
            target += nums[i];
            max = Math.max(max, nums[i]);
        }
        if ((target & 1) == 1) return false; // 奇数
        else target /= 2;
        if (max > target) return false;

        boolean[][] dp = new boolean[n][target + 1]; // 0..i 的数字中是否存在方案使得和为 j
        // 数字 nums[i] 所在的行都能使得和为 nums[i]
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                dp[i][nums[j]] = true;
            }
        }

        // 0..i 中怎么选都能使得和为 0
        for (int i = 0; i < n; i++) {
            dp[i][0] = true;
        }

        // 和为 j 的数字可以由 j - nums[i]（如果存在的话） 得到
        // 和为 j 的数字可以由 j （如果存在的话）得到
        // 可以根据上面的内容对 dp 数组进行填表
        // for (int i = 1; i < n; i++) {
        //     for (int j = 1; j <= target; j++) {

        //         if (j >= nums[i]) {

        //             dp[i][j] = dp[i - 1][j] | dp[i - 1][j - nums[i]];

        //             // 与上面的内容等价
        //             // if (dp[i - 1][j - nums[i]]) {
        //             //     dp[i][j] = true;
        //             // }
        //             // if (dp[i - 1][j]) {
        //             //     dp[i][j] = true;
        //             // }

        //         } else {
        //             dp[i][j] = dp[i - 1][j];

        //             // 与上面的内容等价
        //             if (dp[i - 1][j]) {
        //                 dp[i][j] = true;
        //             }
        //         }
        //     }
        // }

        for (int i = 1; i < n; i++) {
            int num = nums[i];
            for (int j = 1; j <= target; j++) {
                if (j >= num) {
                    dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }

        
        return dp[n - 1][target];
    }
}

优化空间：

和零钱兑换的一个关系：

可以把nums看成是各种零钱组合，整数amount对应这里的target，也就是nums总和的一半。区别在于这里nums里面的值只能用一次。

所以外层遍历都是遍历零钱组合，而内层遍历在遍历amount的时候有一个差别，即分割等和子集是倒着遍历，而零钱是正着遍历。

这里为什么要倒着遍历就是因为这里的值是不能用两遍，而零钱问题中是可以用多遍的，所以从小到大遍历~~

另外一个只判断能否成功一个判断最小零钱只是输出上的差异了。

class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length, target = 0, max = 0;
        for (int i = 0; i < n; i++) {
            target += nums[i];
            max = Math.max(max, nums[i]);
        }
        if ((target & 1) == 1) return false; // 奇数
        else target /= 2;
        if (max > target) return false;

        boolean[] dp = new boolean[target + 1]; // 0..i 的数字中是否存在方案使得和为 j

        dp[0] = true;

        for (int i = 0; i < n; i++) { // 外层枚举数字
            int num = nums[i];
            for (int j = target; j >= num; j--) {
                dp[j] |= dp[j - num];
                // 等价于
                // if (dp[j - num]) {
                //     dp[j] = true;
                // }
            }
        }

        
        return dp[target];
    }
}

最长有效括号

动态规划

0 <= s.length <= 3 * 10^4

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

定义 dp[i] 表示以下标 i 字符结尾的最长有效括号的长度。

难点在于怎么思考状态转移方程。

想到如果是合法的括号，那么肯定是左右都有，那么是不是可以每次走两步

s[i]=‘)’ 且 s[i−1]=‘(’，也就是字符串形如 “……()”，我们可以推出：dp[i]=dp[i−2]+2

key： 两种有效的括号类型：（…）（…）（…），另一种为嵌套格式（（…））

第一种可以 dp[i] = dp[i - 2] + 2，第二种则比较复杂。

考虑第一次遇到 … ））时，需要找到和右括号匹配的左括号，我们这里可以根据最优子结构得到 dp[i - 1] 代表了前一个右括号之前的有效括号，那么 i - dp[i - 1] - 1 的位置就是和当前右括号匹配的位置，如果这个位置是左括号，那么最长有效长度就可以 + 2，否则就不更新。

截屏2020-04-17下午4.26.34.png

同时还要考虑 …((…)) 的情况，也就是加上 dp[i - dp[i - 1] - 2]

于是有以下内容：

class Solution {
    public int longestValidParentheses(String s) {
        int n = s.length();
        int[] dp = new int[n]; // 以下标 i 结尾的最长子串长度
        int max = 0;
        for (int i = 1; i < n; i++) {
            if (s.charAt(i - 1) == '(' && s.charAt(i) == ')') {
                // 能够处理 ..()，但是无法处理 (())
                dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
            } else if (s.charAt(i - 1) == ')' && s.charAt(i) == ')') {
                // 这里处理 ...((...)) 的情况
                // 判断 s[i] 是否有对应的左括号
                if (i - dp[i - 1] - 1 >= 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
                    // 第一项对应 ((...)) 中的三个点
                    // 最后一项是和匹配的括号的情况连起来，对应 ...(()) 中的三个点
                    // dp[i] = dp[i - 1] + 2 + (i - dp[i - 1] - 2) > 0 ? dp[i - dp[i - 1] - 2] : 0;
                    dp[i] = dp[i - 1] + 2 + ((i - dp[i - 1] - 2) > 0 ? dp[i - dp[i - 1] - 2] : 0);
                }
            }
            max = Math.max(max, dp[i]);
        }
        return max;
    }
}

栈

如果用栈，那么关键在于对于 …(…)() 和 …(()) 这两种情况如何判断长度和判断连续。

对于连续来说，可以过一遍字符串即可，对于长度判断，要点在于，如果对于右括号没有对应的左括号时，说明需要另起炉灶，重新计算最大长度。

class Solution {
    public int longestValidParentheses(String s) {
        int max = 0;
        Deque<Integer> stack = new LinkedList<Integer>();
        stack.push(-1);
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') {
                stack.push(i);
            } else {
                stack.pop();
                if (stack.isEmpty()) {
                    stack.push(i);
                } else {
                    max = Math.max(max, i - stack.peek());
                }
            }
        }
        return max;
    }
}

寻找两个正序数组的中位数³

中位数定义：将一个集合划分为两个长度相等的子集，其中一个子集中的元素总是大于另一个子集中的元素。

      left_part          |         right_part
A[0], A[1], ..., A[i-1]  |  A[i], A[i+1], ..., A[m-1]
B[0], B[1], ..., B[j-1]  |  B[j], B[j+1], ..., B[n-1]

根据中位数的定义，我们需要找到以上的划分（设两个数组总长度为偶数）使得

$\text{len}(left_part) = \text{len}(right_part)$
$\max(left_part)=\max(right_part)$

此时的中位数为：

$\text{median} = \frac{\max(left\_part)+\min(right\_part)}{2}$

所以现在的问题关键在于寻找这样一个划分。要寻找这样一个划分需要根据这个划分满足的两个条件：

左边元素共有 $i + j$ 个，右边元素共有 $(m-i)+(n-j)$ 个，所以由第一个式子可以得到 $i+j=(m-i)+(n-j)$。变形得到 $i+j=\frac{m+n}{2}$。假设 $m < n$，即 B 数组长于 A 数组，则 $i\in[0,m]$，有 $j = \frac{m+n}{2}-i$ 且 $j \in [0,n]$，所以只要知道 $i$ 的值，那么 $j$ 的值也是确定的。
在 $(0, m)$ 中找到 $i$，满足 $A[i-1] \le B[j]$ 且 $A[i] \ge B[j-1]$ 。

注意到第一个条件中，当 $i$ 增大的时候，$j$ 会减小以此来保证左右两部分的元素个数相同。同时 A、B 数组都是单调不递减的，所以一定存在一个最大的 $i$ 满足 $A[i-1] \le B[j]$。（当 $i$ 取 $i+1$ 时 $A[i] > B[j-1]$）

所以问题转化为：找一个最大的 $i$ 使得 $A[i-1] \le B[j]$。

对于这个问题，我们容易枚举 $i$，同时 A、B 都是单调递增的，所以我们还能知道枚举出的 $i$ 是不是满足条件（$A[i-1] \le B[j]$），并从中找出满足条件的最大 $i$ 值即可。

对于两个数组总长度为奇数的情况，可以使得 $j = \lfloor \frac{m+n+1}{2}-i \rfloor$。

代码如下：

#[warn(dead_code)]
struct Solution;

impl Solution {
    pub fn find_median_sorted_arrays(nums1: Vec<i32>, nums2: Vec<i32>) -> f64 {
        if nums1.len() > nums2.len() {
            return Solution::find_median_sorted_arrays(nums2, nums1);
        }
        // m < n
        let (m, n) = (nums1.len(), nums2.len());
        let mut left = 0;
        let mut right = m;
        let mut pos = 0;
        let mut median1 = 0;
        let mut median2 = 0;
        while left <= right {
            let i = (left + right) / 2;
            let j = (m + n + 1) / 2 - i;
            let nums_im1 = if i == 0 { -0x3f3f3f3f } else { nums1[i - 1] };
            let nums_i = if i == m { 0x3f3f3f3f } else { nums1[i] };
            let nums_jm1 = if j == 0 { -0x3f3f3f3f } else { nums2[j - 1] };
            let nums_j = if j == n { 0x3f3f3f3f } else { nums2[j] };
            if nums_im1 <= nums_j {
                median1 = std::cmp::max(nums_im1, nums_jm1);
                median2 = std::cmp::min(nums_i, nums_j);
                left = i + 1;
            } else {
                right = i - 1;
            }
        }
        if (m + n) & 1 == 0 {
            (median1 + median2) as f64 / 2.0
        } else {
            median1 as f64
        }
    }
}

三数之和

朴素算法

排序之后三重循环，判断三个数之和是否为 $0$，时间复杂度 $O(n^3)$。

排序的目的是为了容易地去除重复数字，因为排序之后只需要判断当前和前一个元素是否相等就可以知道是否是重复数字。

排序后双指针

注意到排序之后整个数组是单调非递减的，我们需要 $a+b+c=0$，当固定了 $a$ 和 $b$ 的时候，$c$ 从大到小地判断是否有 $a+b+c=0$ 即可。看似是最外层对应 $a$ 的循环嵌套对应 $b$ 的循环，并在其中加上了 $c$ 递减的循环，但是实际上注意到当 $b$ 与 $c$ 是同一个元素时，如果仍然不满足 $a+b+c=0$，那么 $c$ 继续向左减小就与之前的数字重复了，所以对于每一次 $b$ 中的循环，最多运行 $n$ 次，外边再嵌套 $a$ 的循环，时间复杂度为 $O(n^2)$。

代码如下：

#[warn(dead_code)]
struct Solution;

impl Solution {
    pub fn three_sum(mut nums: Vec<i32>) -> Vec<Vec<i32>> {
        nums.sort();
        let len = nums.len();
        let mut ans = Vec::new();
        for i in 0..len {
            // 防止取到相同的数字
            if i > 0 && nums[i - 1] == nums[i] {
                continue;
            }
            let mut third = len - 1;
            // 注意这里开始位置是 i+1，目的是为了不与 a 取重
            for j in i + 1..len {
                // 注意这里判定条件是 j > i+1 否则会取不到与 a 相同的数字
                if j > i + 1 && nums[j - 1] == nums[j] {
                    continue;
                }
                while j < third && nums[i] + nums[j] + nums[third] > 0 {
                    third = third - 1;
                }
                if j == third {
                    break;
                }
                if nums[i] + nums[j] + nums[third] == 0 {
                    ans.push(vec![nums[i], nums[j], nums[third]]);
                }
            }
        }
        ans
    }
}

盛最多水的容器⁴

$area = (right - left) * \min (height[left], height[right])$

由上面的公式可以知道，面积由两部分共同决定：

宽度
高度

所以考虑尽可能地增加宽度和高度。假设左指针指向的数为 $x$，右指针指向的数为 $y$，假设 $x < y$，距离为 $t$，接下来进行具体分析：

水量 $ area = \min(x, y) t = x t $，当左指针不变的时候，右指针无论在哪都不会影响容器的水量了，水量是固定的 $x*t$。
所以考虑左指针向右移动，这样才有可能取到更大的水量。
同理左指针指向的数大于右指针指向的数的时候，左移右指针才有可能取到更大的水量。
重复以上步骤就可以得到最大水量。

总时间复杂度为 $O(n)$。

注解：

对于双指针问题，两个指针的初始位置不一定都在最左或者最右，要灵活地设置指针位置。

最接近三数之和

与「盛最多水的容器」和「三数之和」类似，代码如下：

#[warn(dead_code)]
struct Solution;

impl Solution {
    pub fn three_sum_closest(mut nums: Vec<i32>, target: i32) -> i32 {
        nums.sort();
        let len = nums.len();
        let mut ans = 0;
        let mut diff = 0x3f3f3f3f;
        for i in 0..len {
            if i > 0 && nums[i] == nums[i - 1] {
                continue;
            }
            let mut j = i + 1;
            let mut k = len - 1;
            while j < k {
                //dbg!((i, j , k));
                let sum = nums[i] + nums[j] + nums[k];
                if sum == target {
                    return sum;
                }
                let tmp = (sum - target).abs();
                if tmp < diff {
                    diff = tmp;
                    ans = sum;
                }
                if sum > target {
                    let mut k0 = k - 1;
                    while j < k0 && nums[k0] == nums[k] {
                        k0 = k0 - 1;
                    }
                    k = k0;
                } else {
                    let mut j0 = j + 1;
                    while j0 < k && nums[j0] == nums[j] {
                        j0 = j0 + 1;
                    }
                    j = j0;
                }
            }
        }
        ans
    }
}

最大整除子集

给你一个由 无重复 正整数组成的集合 nums ，请你找出并返回其中最大的整除子集 answer ，子集中每一元素对 (answer[i], answer[j]) 都应当满足：

answer[i] % answer[j] == 0 ，或
answer[j] % answer[i] == 0

如果存在多个有效解子集，返回其中任何一个均可。

动态规划

设子集为 A，题目要求对于任意 (A[i],A[j])，都满足 A[i]modA[j]=0 或者 A[j]modA[i]=0，也就是一个数是另一个数的倍数。

这里有两个条件，不好处理。我们可以把 A 排序，或者说把 nums 排序（从小到大）。由于 nums 所有元素互不相同（没有相等的情况），题目要求变成：

从（排序后的）nums 中选一个子序列，在子序列中，右边的数一定是左边的数的倍数。
由于 x 的倍数的倍数仍然是 x 的倍数，只要相邻元素满足倍数关系，那么任意两数一定满足倍数关系。于是题目要求变成：

从（排序后的）nums 中选一个子序列，在子序列中，任意相邻的两个数，右边的数一定是左边的数的倍数。
这类似 300. 最长递增子序列，都是相邻元素有约束，且要计算的都是子序列的最长长度。

下文把满足题目要求的子序列叫做合法子序列。

class Solution {
    public List<Integer> largestDivisibleSubset(int[] nums) {
        Arrays.sort(nums);
        
        int n = nums.length;
        int[] dp = new int[n]; // 以 nums[i] 结尾的最大整除子集
        int[] from = new int[n];
        Arrays.fill(from, -1);
        int maxI = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] % nums[j] == 0 && dp[j] > dp[i]) {
                    dp[i] = dp[j];
                    from[i] = j;
                }
            }
            dp[i]++;
            if (dp[i] > dp[maxI]) {
                maxI = i; // 最大整除子集最后一个数的下标
            }
        }

        List<Integer> path = new ArrayList<>(dp[maxI]);
        for (int i = maxI; i >= 0; i = from[i]) {
            path.add(nums[i]);
        }
        return path;
    }
}

多维 dp

不同路径

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

二维爬楼梯，对于每个位置能从上面和左边过来。

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];

        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }

        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }

        // 对于一个位置，能从左边或者上面过来
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
            }
        }

        return dp[m - 1][n - 1];
    }
}

最小路径和

还是和不同路径一样，不同的是从左上到右下的时候需要记录最小路径和。还有初始化状态的时候，要记得加上走过来的时候的最小值。

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n]; // 记录到 i, j 的最小数字和

        dp[0][0] = grid[0][0];

        for (int i = 1; i < n; i++) {
            dp[0][i] = grid[0][i] + dp[0][i - 1];
        }

        for (int i = 1; i < m; i++) {
            dp[i][0] = grid[i][0] + dp[i - 1][0];
        }

        // 对于 dp[i][j] 只能从上面或者左边过来，记录最小和就好
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
}

最长回文子串

要点在于：

初始状态所有字符都和自己回文。
dp$$i][j] 表示子串 i…j 是否是回文串。
为了便于考虑边界情况，外层循环枚举 j，内层循环枚举 i。
dp $i][j] 如果是回文字符串，要求 dp$ i + 1][j - 1] 是回文字符串，并且 s[i] == s[j]。

class Solution {
    public String longestPalindrome(String s) {
        int n = s.length();
        // dp[i][j] 表示子串 i...j 是否是回文串 
        boolean dp[][] = new boolean[n][n];
        int maxLen = 0;
        int start = 0, end = 0;
        
        // 状态初始化，自己和自己回文
        for (int i = 0; i < n; i++) {
            dp[i][i] = true;
        }

        for (int j = 0; j < n; j++) {
            for (int i = 0; i < j; i++) {
                if ((j - i <= 1 || dp[i + 1][j - 1]) && s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = true;
                    if (j - i + 1 > maxLen) {
                        maxLen = j - i + 1;
                        start = i;
                        end = j;
                    }
                }
            }
        }
        return s.substring(start, end + 1);
    }
}

最长公共子序列

要点：

dp[i][j] 表示字符串 s1[0…i) 和 s2[0…j) 的最长公共子序列长度，注意这里是左闭右开。
对于 dp[i][j] 能从 dp[i - 1][j - 1] + 1 得到，此时 s1[i] == s2[j]
不相等时 dp[i][j] 是 Math.max(dp[i - 1][j], dp[i][j - 1])，也就是跳过当前字符
这里的 i 从 1…len1，然后 i-1 是 0…len1-1，所以 i-1 遍历了整个字符串。如果不使用这种处理方式，会导致最后一位字符未被处理。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int len1 = text1.length();
        int len2 = text2.length();
        int[][] dp = new int[len1 + 1][len2 + 1]; // 字符串 s1[0...i] 和 s2[0...j] 的最长公共子序列长度
        
        // 对于 dp[i][j] 能从 dp[i - 1][j - 1] + 1 得到，此时 s1[i] == s2[j]
        // 不相等时 dp[i][j] 是 Math.max(dp[i - 1][j], dp[i][j - 1])， 也就是跳过当前字符
        // 注意！！！
        // 这里的 i 从 1...len1，然后 i-1 是 0...len1-1，所以 i-1 遍历了整个字符串
        // 如果不使用这种处理方式，会导致最后一位字符未被处理
        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[len1][len2];
    }
}

编辑距离

要点：

dp[i][j] 表示 word1 前 i 个字符变成 word2 前 j 个字符需要的最少操作数
边界条件是 0 字符和有 i 个字符的情况。
状态转移

1
2
3

从 dp[i - 1][j - 1] 过来是替换掉 word1 中的字符，因为 dp[i - 1][j - 1] 已经匹配
从 dp[i - 1][j] 过来是删除掉 word1 中的字符，因为 dp[i - 1][j] 已经匹配
从 dp[i][j - 1] 过来是删除掉 word2 中的字符（等价于 word1 增加字符），因为 dp[i][j - 1] 已经匹配

class Solution {
    public int minDistance(String word1, String word2) {
        int len1 = word1.length();
        int len2 = word2.length();
        int[][] dp = new int[len1 + 1][len2 + 1]; // word1 前 i 个字符变成 word2 前 j 个字符需要的最少操作数

        for (int i = 1; i <= len1; i++) {
            dp[i][0] = i;
        }

        for (int i = 1; i <= len2; i++) {
            dp[0][i] = i;
        }

        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) { // 不用编辑
                    dp[i][j] = dp[i - 1][j - 1];
                } else { // 编辑 word1 使其变成 word2
                    // 从 dp[i - 1][j - 1] 过来是替换掉 word1 中的字符，因为 dp[i - 1][j - 1] 已经匹配
                    // 从 dp[i - 1][j] 过来是删除掉 word1 中的字符，因为 dp[i - 1][j] 已经匹配
                    // 从 dp[i][j - 1] 过来是删除掉 word2 中的字符（等价于 word1 增加字符），因为 dp[i][j - 1] 已经匹配
                    dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
                }
            }
        }
        return dp[len1][len2];
    }
}

数据结构

合并K个升序链表

使用优先队列即可。

use std::{cmp::Reverse, collections::BinaryHeap};
impl Solution {
    pub fn merge_k_lists(lists: Vec<Option<Box<ListNode>>>) -> Option<Box<ListNode>> {
        let mut priority_queue = BinaryHeap::new();
        let mut ret = Box::new(ListNode::new(0));
        let mut ptr = &mut ret;
        for list in lists {
            let mut plist = &list;
            while let Some(node) = plist {
                priority_queue.push(Reverse(node.val));
                plist = &node.next;
            }
        }

        while let Some(Reverse(node)) = priority_queue.pop() {
            ptr.next = Some(Box::new(ListNode::new(node)));
            ptr = ptr.next.as_mut().unwrap();
        }
        ret.next
    }
}

贪心

有序三元组中的最大值 I

3 <= nums.length <= 100
1 <= nums[i] <= 106

给你一个下标从 0 开始的整数数组 nums 。

请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中，找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数，则返回 0 。

下标三元组 (i, j, k) 的值等于 (nums[i] - nums[j]) * nums[k] 。

数组长度 <= 100，也就是说 n^3 = 1e6，可以暴力：

但是要注意 ans 是 long 的，所以存在超出 int 的情况。

class Solution {
    public long maximumTripletValue(int[] nums) {
        long ans = 0;
        int n = nums.length;
        for (int i = 0; i < n - 2; i++) {
            for (int k = n - 1; k >= i + 2; k--) {
                for (int j = i + 1; j < k; j++) {
                    ans = Math.max(ans, (long)nums[k] * (nums[i] - nums[j]));
                }
            }
        }
        return ans;
    }
}

优化为 O(n^2)，要点在于当固定 j, k 时，i 是 0…j 的最大值，所以 i 可以由 j 动态得到。

class Solution {
    public long maximumTripletValue(int[] nums) {
        long ans = 0;
        int n = nums.length;
        for (int k = 2; k < n; k++) {
            long i = nums[0];
            for (int j = 1; j < k; j++) {
                ans = Math.max(ans, nums[k] * (i - nums[j]));
                i = Math.max(i, nums[j]);
            }
        }        

        return ans;
    }
}

优化为 O(n)，要点在于可以提前维护 0…j 和 j…n 的最大值。

class Solution {
    public long maximumTripletValue(int[] nums) {
        long ans = 0;
        int n = nums.length;
        int[] leftMax = new int[n + 1];
        int[] rightMax = new int[n + 1];
        for (int i = 1; i < n; i++) {
            leftMax[i] = Math.max(leftMax[i - 1], nums[i - 1]);
        }
        for (int i = n - 2; i > 0; i--) {
            rightMax[i] = Math.max(rightMax[i + 1], nums[i + 1]);
        }
        for (int i = 1; i < n - 1; i++) {
            ans = Math.max(ans, (long)rightMax[i] * (leftMax[i] - nums[i]));
        }

        return ans;
    }
}

优化空间为 O(1)，要点在于对于 (nums[i] - nums[j]) * nums[k]，i 和 j 是小于 k 的，所以 i，j 要走的路，k 都走过了，所以可以枚举 k 的时候维护其他状态。

然后维护其他状态的思路是考虑固定 k，如果要枚举 k，那么考虑 k 被固定的情况，其他的两个变量如何变化。

维护 nums[i] - nums[j] 的最大值，维护 nums[i] 的最大值。

class Solution {
    public long maximumTripletValue(int[] nums) {
        long ans = 0;
        int n = nums.length;
        int maxI = 0;
        int maxISubJ = 0;
        for (int k = 0; k < n; k++) {
            ans = Math.max(ans, (long)maxISubJ * nums[k]);
            maxISubJ = Math.max(maxISubJ, maxI - nums[k]);
            maxI = Math.max(maxI, nums[k]);
        }

        return ans;
    }
}

使数组元素互不相同所需的最少操作次数

给你一个整数数组 nums，你需要确保数组中的元素 互不相同 。为此，你可以执行以下操作任意次：

从数组的开头移除 3 个元素。如果数组中元素少于 3 个，则移除所有剩余元素。

注意：空数组也视作为数组元素互不相同。返回使数组元素互不相同所需的 最少操作次数 。

模拟

class Solution {
    public int minimumOperations(int[] nums) {
        int n = nums.length;
        int[] c = new int[101];
        for (int i = 0; i < n; i++) {
            c[nums[i]]++;
        }
        int ans = 0;
        for (int i = 0; i < n; i+=3) {
            boolean ok = true;
            for (int j = 1; j <= 100; j++) {
                if (c[j] > 1) {
                    c[nums[i]]--;
                    if (i + 1 < n) c[nums[i+1]]--;
                    if (i + 2 < n) c[nums[i+2]]--;
                    ok = false;
                    break;
                }
            }
            if (!ok) ans++;
        }
        return ans;
    }
}

技巧

class Solution {
    public int minimumOperations(int[] nums) {
        // 倒序遍历
        int n = nums.length;
        int ans = n / 3;
        boolean[] seen = new boolean[101];
        for (int i = n - 1; i >= 0; i--) {
            if (seen[nums[i]]) {
                return i / 3 + 1;
            }
            seen[nums[i]] = true;
        }
        return 0;
    }
}

数学

找出所有子集的异或总和再求和

简单做法

枚举所有子集，然后求出异或总和

class Solution {
    public int subsetXORSum(int[] nums) {
        int n = nums.length;
        int ans = 0;
        for (int i = 0; i < (1 << n); i++) {
            int XORSum = 0;
            for (int j = 0; j < n; j++) {
                if ((i & (1 << j)) != 0) {
                    XORSum = XORSum ^ nums[j];
                }
            }
            ans += XORSum;
        }
        return ans;
    }
}

数学做法

提示1

对于异或运算，每个比特位是互相独立的，我们可以先思考只有一个比特位的情况，也就是 nums 中只有 0 和 1 的情况。（从特殊到一般）

在这种情况下，如果子集中有偶数个 1，那么异或和为 0；如果子集中有奇数个 1，那么异或和为 1。所以关键是求出异或和为 1 的子集个数。题目要求的是子集的异或总和再求和，异或和为 1 的子集的个数就是最终答案。

设 nums 的长度为 n，且包含 1。我们可以先把其中一个 1 拿出来，剩下 n−1 个数随便选或不选，有 $2^{n−1}$ 种选法。

如果这 n−1 个数中选了偶数个 1，那么放入我们拿出来的 1（选这个 1），得到奇数个 1，异或和为 1。
如果这 n−1 个数中选了奇数个 1，那么不放入我们拿出来的 1（不选这个 1），得到奇数个 1，异或和为 1。

所以，恰好有 $2^{n−1}$ 个子集的异或和为 1。

注意这个结论与 nums 中有多少个 1 是无关的，只要有 1，异或和为 1 的子集个数就是 $2^{n−1}$。如果 nums 中没有 1，那么有 0 个子集的异或和为 1。

所以，在有至少一个 1 的情况下，nums 的所有子集的异或和的总和为 $2^{n−1}$。

提示2

推广到多个比特位的情况。

例如 $nums = [3,2,8]$，3 = 11，2 = 10，8 = 1000

第 $0,1,3$ 个比特位上有 $1$，每个比特位对应的「所有子集的异或和的总和」分别为

$2^0\cdot2^{n - 1}, 2^1\cdot2^{n - 1}, 2^3\cdot2^{n - 1}$

相加得

$(2^0 + 2^1 + 2^3)\cdot2^{n - 1}$

怎么知道哪些比特位上有 $1$？计算 $nums$ 的所有元素的 OR，即 $1011_{(2)}$。

注意到，所有元素的 OR，就是上例中的 $2^0 + 2^1 + 2^3$。

一般地，设 $nums$ 所有元素的 OR 为 $or$，$nums$ 的所有子集的异或和的总和为

$or\cdot2^{n - 1}$

class Solution {
    public int subsetXORSum(int[] nums) {
        int n = nums.length;
        int XORSum = 0;
        for (int i = 0; i < n; i++) {
            XORSum = XORSum | nums[i]; 
        }
        return XORSum * 1 << (n - 1);
    }
}

数位 dp

统计强大整数的数目

给你三个整数 start ，finish 和 limit 。同时给你一个下标从 0 开始的字符串 s ，表示一个正整数。

如果一个正整数 x 末尾部分是 s （换句话说，s 是 x 的后缀），且 x 中的每个数位至多是 limit ，那么我们称 x 是 强大的 。

请你返回区间 [start..finish] 内强大整数的 总数目 。

如果一个字符串 x 是 y 中某个下标开始（包括 0 ），到下标为 y.length - 1 结束的子字符串，那么我们称 x 是 y 的一个后缀。比方说，25 是 5125 的一个后缀，但不是 512 的后缀。

组合数学

我们可以实现一个计数函数 calculate(x) 来直接计算小于等于 x 的满足 limit 的数字数量，然后答案即为 calculate(finish) - calculate(start - 1)。首先考虑 x 中与 s 长度相等的后缀部份（如果 x 长度小于 s，答案为 0），如果 x 的后缀大于等于 s，那么后缀部份对答案贡献为 1。接着考虑剩余的前缀部份。令 preLen 表示前缀的长度，即 |x| - |s|。对于前缀的每一位 x[i]： - 如果超过了 limit，意味着当前位最多只能取到 limit，后面的所有位任取组成的数字也不会超过 x。因此包括第 i 位，后面的所有位（共 preLen - i 位）都可以取 [0, limit]（共 limit + 1 个数），对答案的贡献是 (limit + 1)^(preLen - i)。 - 如果 x[i] 没有超过 limit，那么当前位最多取到 x[i]，后面的所有位可以取 [0, limit]，对答案的贡献是 x[i] × (limit + 1)^(preLen - i - 1)。

class Solution {
    public long numberOfPowerfulInt(long start, long finish, int limit, String s) {
        String StrFinish = String.valueOf(finish);
        String StrStart = String.valueOf(start - 1);
        return calculate(StrFinish, s, limit) - calculate(StrStart, s, limit);
    }

    // 计算计算小于等于 x 的满足 limit 的数字数量
    private long calculate(String x, String s, int limit) {
        if (x.length() < s.length()) {
            return 0;
        }
        if (x.length() == s.length()) {
            return x.compareTo(s) >= 0 ? 1 : 0;
        }
        String suffix = x.substring(x.length() - s.length()); // begin index
        long count = 0;
        int preLen = x.length() - s.length();
        for (int i = 0; i <= preLen; i++) {
            int digit = x.charAt(i) - '0';
            if (limit < digit) {
                count += (long) Math.pow(limit + 1, preLen - i);
                return count;
            }
            count += (long)digit * (long)Math.pow(limit + 1, preLen - 1 - i);
        }
        if (suffix.compareTo(s) >= 0) {
            count++;
        }
        return count;
    }
}

数位 dp

定义 dfs(i, limitLow, limitHigh) 表示构造第 i 位及其之后数位的合法方案数，其余参数的含义为：

limitHigh 表示当前是否受到了 finish 的约束（我们要构造的数字不能超过 finish）。若为真，则第 i 位填入的数字至多为 finish[i]，否则至多为 9，这个数记作 hi。如果在受到约束的情况下填了 finish[i]，那么后续填入的数字仍会受到 finish 的约束。例如 finish = 123，那么 i = 0 填的是 1 的话，i = 1 的这一位至多填 2。
limitLow 表示当前是否受到了 start 的约束（我们要构造的数字不能低于 start）。若为真，则第 i 位填入的数字至少为 start[i]，否则至少为 0，这个数记作 lo。如果在受到约束的情况下填了 start[i]，那么后续填入的数字仍会受到 start 的约束。

枚举第 i 位填什么数字。

如果 i < n - |s|，那么可以填 [lo, min(hi, limit)] 内的数，否则只能填 s[i - (n - |s|)]。这里 |s| 表示 s 的长度。

为什么不能把 hi 置为 min(hi, limit)？

1	`int hi = limitHigh ? Math.min(high[i] - '0', limit) : 9;`

你就隐含地说：hi 是由 limit 限制的，而不是由 high 限制的，这就导致之后的 limitHigh && d == hi 判断会出错！

举个例子：

假设 high = 5299, 当前正在处理第 1 位（从左往右），也就是处理 2，而 limit = 1。

如果你写：

1	`hi = Math.min(2, 1) = 1`

你会枚举 0,1 而不是原本允许的 0,1,2，并且还会让 limitHigh && d == hi 在本应为 d==2 时失效！

正确的逻辑应该是：

hi 始终由 limitHigh ? high[i] : 9 来决定；
limit 是附加的“过滤”逻辑，不应该影响 Digit DP 的状态定义；
在枚举循环内部使用 Math.min(hi, limit) 来限制合法的数位；
这样才能确保转移关系和 memo 的缓存是准确的。

递归终点：dfs(n, *, *) = 1，表示成功构造出一个合法数字。

递归入口：dfs(0, true, true)，表示：

从最高位开始枚举。
一开始要受到 start 和 finish 的约束（否则就可以随意填了，这肯定不行）。

class Solution {
    public long numberOfPowerfulInt(long start, long finish, int limit, String s) {
        String low = String.valueOf(start);
        String high = String.valueOf(finish);
        int n = high.length();
        low = "0".repeat(n - low.length()) + low; // 补前导零，和 high 对齐
        long[] memo = new long[n];
        Arrays.fill(memo, -1);
        return dfs(0, true, true, low.toCharArray(), high.toCharArray(), limit, s.toCharArray(), memo);
    }

    private long dfs(int i, boolean limitLow, boolean limitHigh, char[] low, char[] high, int limit, char[] s, long[] memo) {
        if (i == high.length) return 1;

        if (!limitLow && !limitHigh && memo[i] != -1) {
            return memo[i];
        }

        // 第 i 个数位可以从 lo 枚举到 hi
        // 如果对数位还有其它约束，应当只在下面的 for 循环做限制，不应修改 lo 或 hi
        int lo = limitLow ? low[i] - '0' : 0;
        int hi = limitHigh ? high[i] - '0' : 9;

        long res = 0;
        if (i < high.length - s.length) { // 枚举这个数位填什么
            for (int d = lo; d <= Math.min(hi, limit); d++) {
                res += dfs(i + 1, limitLow && d == lo, limitHigh && d == hi, low, high, limit, s, memo);
            }
        } else {
            int x = s[i - (high.length - s.length)] - '0';
            if (lo <= x && x <= hi) { // 题目保证 x <= limit，无需判断
                res = dfs(i + 1, limitLow && x == lo, limitHigh && x == hi, low, high, limit, s, memo);
            }
        }

        if (!limitLow && !limitHigh) {
            memo[i] = res; // 记忆化 (i,false,false)
        }
        return res;
    }
}

统计对称整数的数目

暴力判断 O((high−low)loghigh)

数位 dp

class Solution {
    private char[] lowS, highS;
    private int n, m, diffLh;
    private int[][][] memo;

    public int countSymmetricIntegers(int low, int high) {
        lowS = String.valueOf(low).toCharArray();
        highS = String.valueOf(high).toCharArray();
        n = highS.length;
        m = n / 2;
        diffLh = n - lowS.length;

        memo = new int[n][diffLh + 1][m * 18 + 1]; // 注意 start <= diffLh
        for (int[][] mat : memo) {
            for (int[] row : mat) {
                Arrays.fill(row, -1);
            }
        }

        // 初始化 diff = m * 9，避免出现负数导致 memo 下标越界
        return dfs(0, -1, m * 9, true, true);
    }

    private int dfs(int i, int start, int diff, boolean limitLow, boolean limitHigh) {
        if (i == n) {
            return diff == m * 9 ? 1 : 0;
        }

        // start 当 isNum 用
        if (start != -1 && !limitLow && !limitHigh && memo[i][start][diff] != -1) {
            return memo[i][start][diff];
        }

        int lo = limitLow && i >= diffLh ? lowS[i - diffLh] - '0' : 0;
        int hi = limitHigh ? highS[i] - '0' : 9;

        // 如果前面没有填数字，且剩余数位个数是奇数，那么当前数位不能填数字
        if (start < 0 && (n - i) % 2 > 0) {
            // 如果必须填数字（lo > 0），不合法，返回 0
            return lo > 0 ? 0 : dfs(i + 1, start, diff, true, false);
        }

        int res = 0;
        boolean isLeft = start < 0 || i < (start + n) / 2;
        for (int d = lo; d <= hi; d++) {
            res += dfs(i + 1,
                       start < 0 && d > 0 ? i : start, // 记录第一个填数字的位置
                       diff + (isLeft ? d : -d), // 左半 +，右半 -
                       limitLow && d == lo,
                       limitHigh && d == hi);
        }

        if (start != -1 && !limitLow && !limitHigh) {
            memo[i][start][diff] = res;
        }
        return res;
    }
}

树状数组

统计数组中好三元组数目

给你两个下标从 0 开始且长度为 n 的整数数组 nums1 和 nums2 ，两者都是 [0, 1, ..., n - 1] 的排列。

好三元组 指的是 3 个 互不相同 的值，且它们在数组 nums1 和 nums2 中出现顺序保持一致。换句话说，如果我们将 pos1v 记为值 v 在 nums1 中出现的位置，pos2v 为值 v 在 nums2 中的位置，那么一个好三元组定义为 0 <= x, y, z <= n - 1 ，且 pos1x < pos1y < pos1z 和 pos2x < pos2y < pos2z 都成立的 (x, y, z) 。

请你返回好三元组的 总数目 。

示例 1：

输入：nums1 = [2,0,1,3], nums2 = [0,1,2,3]
输出：1
解释：
总共有 4 个三元组 (x,y,z) 满足 pos1x < pos1y < pos1z ，分别是 (2,0,1) ，(2,0,3) ，(2,1,3) 和 (0,1,3) 。
这些三元组中，只有 (0,1,3) 满足 pos2x < pos2y < pos2z 。所以只有 1 个好三元组。

示例 2：

1
2
3

输入：nums1 = [4,0,1,3,2], nums2 = [4,1,0,2,3]
输出：4
解释：总共有 4 个好三元组 (4,0,3) ，(4,0,2) ，(4,1,3) 和 (4,1,2) 。

题意解读

题目本质上是求：nums1 和 nums2 的长度恰好为 3 的公共子序列的个数。

你可能想到了 [1143. 最长公共子序列]。但本题 $n$ 太大，写 $O(n^2)$ 的 DP 太慢。

核心思路

本题是排列，所有元素互不相同。如果可以通过某种方法，把 nums1 变成 [0,1,2, ... ,n - 1]，我们就能把「公共子序列问题」变成「严格递增子序列问题」，后者有更好的性质，可以更快地求解。

此外，本题子序列长度为 3，对于 3 个数的问题，通常可以枚举中间那个数。

前置知识：置换

置换是一个排列到另一个排列的双射。

以示例 2 为例，定义如下置换 $P(x)$：

$\begin{pmatrix} x & 0 & 1 & 2 & 3 & 4 \\ P(x) & 1 & 2 & 4 & 3 & 0 \end{pmatrix}$

把 nums1 = [4,0,1,3,2] 中的每个元素 $x$ 替换为 $P(x)$，可以得到一个单调递增的排列 $A = [0,1,2,3,4]$。把 $P(x)$ 应用到 nums2 = [4,1,0,2,3] 上，可以得到一个新的排列 $B = [0,2,1,4,3]$。

在置换之前，(4,0,3) 是两个排列的公共子序列。

在置换之后，$(P(4),P(0),P(3)) = (0,1,3)$ 也是两个新的排列的公共子序列。

⚠️注意：置换不是排序，是映射（可以理解成重命名），原来的公共子序列在映射后，子序列元素的位置没变，只是数值变了，仍然是公共子序列。所以置换不会改变公共子序列的个数。

思路

把 nums1 置换成排列 $A = [0,1,2, … ,n - 1]$，设这一置换为 $P(x)$。把 $P(x)$ 也应用到 nums2 上，得到排列 $B$。

置换后，我们要找的长为 3 的公共子序列，一定是严格递增的。由于 $A$ 的所有子序列都是严格递增的，我们只需关注 $B$。现在问题变成：

$B$ 中有多少个长为 3 的严格递增子序列？

对于长为 3 的严格递增子序列 $(x,y,z)$，枚举中间元素 $y$。现在问题变成：

在 $B$ 中，元素 $y$ 的左侧有多少个比 $y$ 小的数 $x$？右侧有多少个比 $y$ 大的数 $z$？

枚举 $y = B[i]$，设 $i$ 左侧有 $less_y$ 个元素比 $y$ 小，那么 $i$ 左侧有 $i - less_y$ 个元素比 $y$ 大。在整个排列 $B$ 中，比 $y$ 大的数有 $n - 1 - y$ 个，减去 $i - less_y$，得到 $i$ 右侧有 $n - 1 - y - (i - less_y)$ 个数比 $y$ 大。所以（根据乘法原理）中间元素是 $y$ 的长为 3 的严格递增子序列的个数为：

$ less_y \cdot (n - 1 - y - (i - less_y)) $

枚举 $y = B[i]$，计算上式，加入答案。

如何计算 $less_y$ ？这可以用值域树状数组（或者有序集合）。

值域树状数组的意思是，把元素值视作下标。添加一个值为 3 的数，就是调用树状数组的 update(3,1)。查询小于 3 的元素个数，即小于等于 2 的元素个数，就是调用树状数组的 pre(2)。

由于本题元素值是从 0 开始的，但树状数组的下标是从 1 开始的，所以把元素值转成下标，要加一。

class FenwickTree {
    private final int[] tree;

    public FenwickTree(int n) {
        tree = new int[n + 1]; // 使用下标 1 到 n
    }

    // a[i] 增加 val
    // 1 <= i <= n
    public void update(int i, long val) {
        for (; i < tree.length; i += i & -i) {
            tree[i] += val;
        }
    }

    // 求前缀和 a[1] + ... + a[i]
    // 1 <= i <= n
    public int pre(int i) {
        int res = 0;
        for (; i > 0; i &= i - 1) {
            res += tree[i];
        }
        return res;
    }
}

class Solution {
    public long goodTriplets(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int[] p = new int[n];
        for (int i = 0; i < n; i++) {
            p[nums1[i]] = i;
        }

        long ans = 0;
        FenwickTree t = new FenwickTree(n);
        for (int i = 0; i < n - 1; i++) {
            int y = p[nums2[i]];
            int less = t.pre(y);
            ans += (long) less * (n - 1 - y - (i - less));
            t.update(y + 1, 1);
        }
        return ans;
    }
}

参考

¹. https://leetcode-cn.com/problems/longest-palindromic-substring/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-bao-gu ↩

². https://oi-wiki.org/string/manacher/ ↩

³. https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-s-114/ ↩

⁴. https://leetcode-cn.com/problems/container-with-most-water/solution/sheng-zui-duo-shui-de-rong-qi-by-leetcode-solution/ ↩

本文作者：EnableAsync
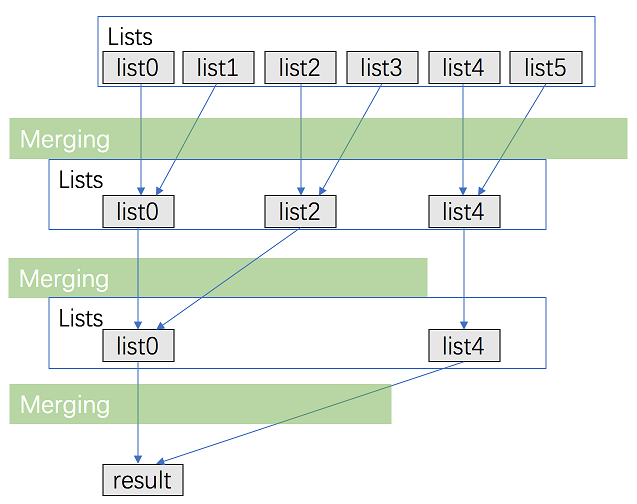
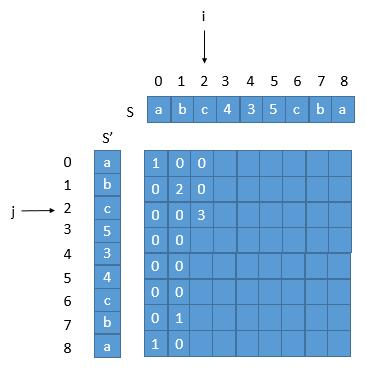
本文链接：https://enableasync.github.io/uncategorized/leetcode/index.html
版权声明：本博客所有文章均采用 BY-NC-SA 许可协议，转载请注明出处！

算法整理

注意事项

rust 中 dbg! 超时

数组

双指针

滑动窗口

前缀和

Java 多组输入示例

模拟矩阵

最大子数组和

合并区间

轮转数组

除自身以外数组的乘积

没有优化

优化空间

缺失的第一个正数

矩阵

矩阵置零

旋转图像

搜索二维矩阵 II

二分

Z 字搜索

双指针

移动零

盛最多水的容器

接雨水

动态规划

单调栈

双指针

滑动窗口

滑动窗口模板

无重复字符的最长子串

找到字符串中所有字母异位词

统计好子数组的数目

区间

合并区间

区间列表的交集

链表

K 个一组翻转链表

排序链表

合并 K 个升序链表

朴素做法

二分做法

二叉树

二叉树的中序遍历

二叉树的最大深度

反转二叉树

对称二叉树

二叉树的直径

二叉树层序遍历

将有序数组转换为二叉搜索树

验证二叉搜索树

二叉搜索树中第 K 小的元素

二叉树的右视图

二叉树展开为链表

递归

迭代1

迭代2

路径总和 III

穷举 O(N^2)

前缀和优化 O(N)

二叉树的最近公共祖先

暴力递归做法

改进递归做法

记录父节点的做法

二叉树中的最大路径和

最深叶节点的最近公共祖先

暴力递归

改进的递归

图论

岛屿数量

腐烂的橘子

单源 bfs

多源 bfs

Trie 树

HashMap 实现

正常实现

课程表

课程表 II

BFS

`rust` 中 `dbg!` 超时